Tout (v)oir /
(c)acher
sinon cliquer sur les items ci dessous pour voir/cacher individuellement leur contenu.
Contenu de l'enseignement
L'espace
Commentaires préalables
Produits scalaire, vecteur et mixte en coordonnées cartésiennes
Lieux, description paramétrique des :
ligne,
nappe et
domaine
Lieux : description implicite
Lieux, description qualitative :
des domaines et leur connexité et
description implicite des domaines
Symétries
Le temps, la cinématique
Les champs de scalaires
Ce que peut représenter un champ de scalaires
Comment former des quantités à partir de leurs densités
Flux
:
advectif et
conductif
Green-Ostrogradski
Équations d'advection, de diffusion et d'advection-diffusion
Généralités sur les calculs effectifs
Équations au dérivées partielles
Équation de diffusion
Équation de Laplace
Exercices
Support du cours du mardi 12 janvier
Quelques éléments essentiels à comprendre
Support du cours du vendredi 15 janvier
Examen 2021
Examen 2022
Contenu de l'enseignement
Cet enseignement a pour fonction de rappeler/introduire les notions de mathématiques utiles pour décrire des dispositifs physiques qui peuvent être modélisés par des équations différentielles ordinaire ou des équations aux dérivées partielles.
Il intervient en 1ière année de l'ENSGSI, au 1ier semestre. Et donc il s'adresse à des élèves qui ont des acquis de base de 1ier cycle ou classes préparatoires.
Son contenu vise d'abord à permettre de comprendre les géométries analytique et différentielle dans l'espace à 3 dimensions en insistant sur la spécification de la représentation d'objets réels.
La tactique utilisée est de ne pas partir d'une base de prérequis très importante et de tenter de montrer comment construire ces objets de manière relativement élémentaire.
Évidemment, l'inconvénient de cela est le renoncement à la précision qu'eût apporté une approche plus synthétique. Et dans de nombreux endroits cette précision est remplacée par un flou assez heuristique (pour ne pas dire que certaines affirmations peuvent être prises en défaut par les contres exemples ad hoc).
Mais on espère néanmoins que le gain --amener les étudiants à une approche pragmatique et active des problèmes mathématiques qui correspondent aux activités de reprėsentation quantitative des phénomènes physiques-- compensera cet inconvénient.
L'espace et ses objets n'est pas intéressant pour l'ingénieur tant qu'il n'y introduit pas de mouvement. La deuxième partie porte donc sur l'introduction du mouvement qui est réalisée avec une tactique similaire.
Et finalement les problèmes de diffusion et d'advection sur une densité scalaire sont introduits dans une dernière partie qui comporte également une introduction aux transformées de Fourier et de Laplace.
Commentaires préalables
La représentation mathématique ad hoc pour l'espace sensible serait a priori celle de l'espace ponctuel euclidien. Mais dès lors qu'une origine est fixée celui-ci s'identifie à l'espace vectoriel euclidien de dimension 3, appelé  . Aussi l'espace ponctuel est-il assimilé à l'espace vectoriel. Et c'est cet espace vectoriel qui est utilisé pour représenter l'espace sensible.
. Aussi l'espace ponctuel est-il assimilé à l'espace vectoriel. Et c'est cet espace vectoriel qui est utilisé pour représenter l'espace sensible.
Parce qu'ils représenteront des objets réels (ou des abstractions de ces objets), il est intéressant d'introduire des propriétés reliants certains points de l'espace à d'autres. Cette relation permet alors de sélectionner ces points comme un ensemble qu'on appelle (selon une terminologie un peu ancienne) un lieu de l'espace.
Trois types de lieux de l'espace particulièrement utiles sont étudiés : les lignes, nappes et domaines. Puisqu'il s'agit des courbes dans l'espace, des surfaces et des volumes, la sémantique peut paraître curieuse : elle a été utilisée, par exemple pour les nappes, pour permettre de distinguer entre « surface » l'ensemble de points qui la constitue et « surface » la mesure de cette « surface ».
L'étude consiste à définir paramétriquement les lieux puis à donner des définitions implicites et finalement à fournir tout un vocabulaire permettant leur description qualitative.
Certaines notions mathématiques s'introduisent lors de l'étude. On a tenté à la fois de les définir à la volée et de fournir les liens (essentiellement vers wikipedia pour ne pas dire uniquement) où elles peuvent être approfondies en cas de besoin.
Pour finir sur les commentaires, il n'est pas impossible que certains trouvent cette matière ardue. Elle l'est ! Mais les raisons de ces difficultés ne viennent pas tant d'un inexplicable préjugé en faveur de l'abstraction vaine que du fait que les objets réels de l'espace réel ne se laissent pas représenter si aisément par un formalisme qui autorise le calcul et par là même la possibilité de les manipuler par la pensée. Ce genre de manipulations étant le cœur même de la pratique de l'ingénieur.
Produits scalaire, vecteur et mixte en coordonnées cartésiennes
Un point de l'espace est donc un élément 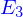 ; on le note avec une flèche surlignante
; on le note avec une flèche surlignante 
Il est possible de manipuler de façon abstraite les éléments de 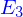 à partir de la définition de l'espace vectoriel auquel on ajoute une structure euclidienne.
à partir de la définition de l'espace vectoriel auquel on ajoute une structure euclidienne.
Un résultat (parmi d'autres) de ces manipulations est qu'on peut introduire une base orthonormée de l'espace 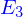 , appelons là
, appelons là 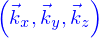 et alors les vecteurs de
et alors les vecteurs de 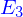 sont de la forme
sont de la forme 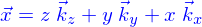 où
où 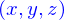 sont appelées les coordonnées cartésiennes du vecteur
sont appelées les coordonnées cartésiennes du vecteur 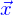
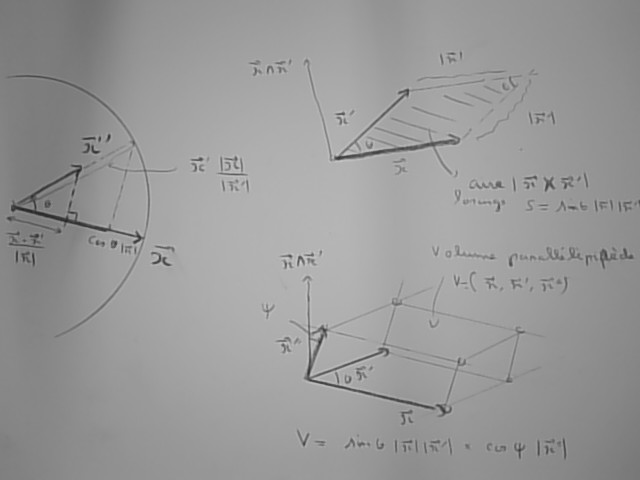
Dire que la base 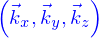 est orthonormée signifie que leurs produits scalaires sont tels que
est orthonormée signifie que leurs produits scalaires sont tels que
c'est une opération symétrique.
Et donc le produit scalaire des vecteurs 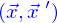 est
est
c'est le produit scalaire euclidien,
À partir de ce produit scalaire, on définit la norme (euclidienne) d'un vecteur comme
S'il est entendu que l'espace 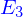 est l'espace des positions, l'unité physique de ses éléments est le mètre. Il serait donc cohérent de faire porter cette unité par les vecteurs de base, les coordonnées étant des nombres sans dimension qui fixeraient la quantité d'unité de longueur portée par les vecteurs de base.
est l'espace des positions, l'unité physique de ses éléments est le mètre. Il serait donc cohérent de faire porter cette unité par les vecteurs de base, les coordonnées étant des nombres sans dimension qui fixeraient la quantité d'unité de longueur portée par les vecteurs de base.
Mais ce n'est pas si commode dans la pratique, aussi préfère-t'on que ce soient les coordonnées qui portent l'unité de longueur alors que les vecteurs de base sont eux sans dimension. Bien évidemment, cela entraîne une certaine incohérence dès lors qu'on a affirmé que les vecteurs de base étaient des éléments de l'espace 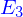 .
.
Nous choisirons supporter cette incohérence plutôt que de chercher à l'élucider, ce qui aurait entraîné une certaine lourdeur qu'on préfère éviter.
Une seconde opération entre vecteurs est le produit vectoriel qu'on définit à partir des vecteurs de base comme
c'est une opération antisymétrique.
Le produit vectoriel entre 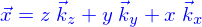 et
et  peut se calculer simplement à partir du déterminant
peut se calculer simplement à partir du déterminant
où on place sur les deux premières lignes les cordonnées des deux vecteurs, la dernière ligne étant formée à partir des vecteurs de base.
La dernière opération entre vecteur est le produit mixte. Sa définition à partir des vecteurs de base est un peu longue à écrire explicitement mais facile à décrire : si 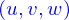 est une permutation paire des
est une permutation paire des 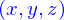 , le produit mixte
, le produit mixte 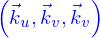 vaut 1 ; si c'est une permutation impair, il vaut -1 ; et si deux quelconques de ces vecteurs sont égaux, il vaut 0.
vaut 1 ; si c'est une permutation impair, il vaut -1 ; et si deux quelconques de ces vecteurs sont égaux, il vaut 0.
Pratiquement le produit mixte des 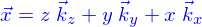 ,
,  et
et 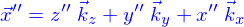 se calcule comme le déterminant
se calcule comme le déterminant
Le produit mixte est relié aux produits scalaire et vectoriel par
Les produits scalaire, vectoriel et mixte permettent l'expression analytique de grandeurs géométriques (la longueur d'un segment projeté sur un autre, l'aire du parallélogramme de bases formées par deux segments, le volume d'un parallélépipède de bases formées par trois segments)
ce qu'il convient de ne jamais oublier.
Description paramétrique de la ligne
Une ligne peut être définie de plusieurs façons, mais on va se limiter ici à la représentation paramétrique : c'est l'image de l'intervalle 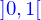 par une application
par une application
qui est donnée. La valeur de l'application peut être représentée par ses coordonnées cartésiennes où s'introduisent les fonctions coordonnées
Il est nécessaire de munir ces fonctions de propriétés minimales pour obtenir ainsi un lieu de l'espace qui ressemble à l'idée intuitive qu'on se fait d'une ligne dans l'espace, quelque chose comme cela
Les propriétés sont :
- la continuité des
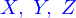 . Sans elle, la ligne comporte plusieurs morceaux, elle est dite non connexe.
. Sans elle, la ligne comporte plusieurs morceaux, elle est dite non connexe.
- la différentiabilité des
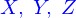 . Sans elle, la ligne n'admet pas de tangente.
. Sans elle, la ligne n'admet pas de tangente.
- la contrainte que les dérivées des
 ne s'annulent pas simultanément. Sinon il y a des points de rebroussement.
ne s'annulent pas simultanément. Sinon il y a des points de rebroussement.
- L'injectivité de la fonction
 . Sinon il y a des points doubles ou pire encore.
. Sinon il y a des points doubles ou pire encore.
On voit donc que l'étude générale des lignes est un chapitre en soi des mathématiques. Mais on cherchera moins l'exhaustivité en la matière qu'une saine compréhension des notions minimales permettant de manipuler des lignes en vue d'applications concrètes.
Ceci étant dit, on n'a pas précisé ce qu'est la dérivée de la fonction 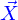 . C'est la fonction
. C'est la fonction
Cette fonction existe si les limites existent pour chacunes des fonctions  et lorsqu'elles existent pour tout les
et lorsqu'elles existent pour tout les  de l'intervalle
de l'intervalle 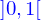 on dit que ces fonctions sont dérivables dans cet intervalle.
on dit que ces fonctions sont dérivables dans cet intervalle.
Lorsque la fonction 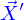 existe, on peut associer à chacun des points
existe, on peut associer à chacun des points 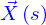 une droite qui est une nouvelle ligne définie paramétriquement comme indiqué sur la figure. Cette droite est appelée la droite tangente à la ligne en
une droite qui est une nouvelle ligne définie paramétriquement comme indiqué sur la figure. Cette droite est appelée la droite tangente à la ligne en 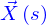 .
.
Et la droite tangente est intéressante notamment parce qu'elle peut être vue comme une approximation de la ligne autour du point 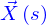 ; c'est à dire que pour les positions suffisamment proches de
; c'est à dire que pour les positions suffisamment proches de  la ligne ne diffère pas sensiblement de sa droite tangente en cette position.
la ligne ne diffère pas sensiblement de sa droite tangente en cette position.
Après cela, il est temps d'insister sur la distinction entre les points de la ligne et la paramétrisation particulière qui permet de générer ces points. Si plutôt que
on avait donné
où
est une fonction continue, différentiable et bijective de son ensemble de départ à son ensemble d'arrivée, on aurait obtenu exactement la même ligne mais avec une paramétrisation différente.
Cela porte à demander que la droite tangente en un point de la ligne soit définie de manière qui ne dépende pas de la paramétrisation particulière qui a servi à construire cette ligne.
Pour cela, il suffit d'utiliser comme vecteur directeur de la droite tangente, le vecteur
et comme ce vecteur est le vecteur tangent à la ligne en 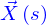 de ne pas le faire dépendre de
de ne pas le faire dépendre de  mais de
mais de 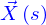 , soit d'introduire
, soit d'introduire
Pour examiner ce que devient ce vecteur avec la paramétrisation  , on peut écrire (par la dérivation de fonction composées)
, on peut écrire (par la dérivation de fonction composées)
d'où vient que
Si on nomme abstraitement 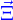 un point de la ligne (qui peut être obtenu par une paramétrisation de celle-ci comme
un point de la ligne (qui peut être obtenu par une paramétrisation de celle-ci comme 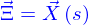 ), on peut donc lui associer le vecteur tangent à la ligne qui est
), on peut donc lui associer le vecteur tangent à la ligne qui est 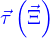 (ce vecteur pouvant être obtenu par la paramétrisation comme
(ce vecteur pouvant être obtenu par la paramétrisation comme 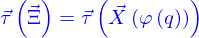 ).
).
Ces considérations permettent de parler d'une ligne, des vecteurs tangents en ses points et des droites tangentes qu'ils génèrent sans nécessairement introduire de paramétrisation. Lorsqu'on le fait, on sait qu'il suffit d'introduire une paramétrisation pour obtenir des expressions de calcul concrètes.
Description paramétrique de la nappe
Comme pour les lignes, on va se limiter à la représentation paramétrique des nappes. Le terme « nappe » a été utilisé pour « surface » qui lui sera réservé pour désigner la mesure d'une portion de nappe.
Dans cette représentation paramétrique, une nappe est l'image de l'intervalle 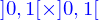 par une application
par une application
qui est donnée. La valeur de l'application peut être représentée par ses coordonnées cartésiennes où s'introduisent les fonctions coordonnées
Ces fonctions coordonnées, sont des fonctions à valeur réelle mais dépendant de deux variables réelles. Cela entraîne une difficulté de calcul supplémentaire par rapport aux lignes, mais on va voir cela par étapes.
Tout d'abord, la nappe peut être vue comme un ensemble de lignes (on dit une famille). Considérons ce dessin
Les lignes indexées du dessin sont :
-
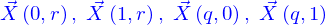 : ces lignes sont les lignes extrémités de la nappe, on dit que l'ensemble qu'elles forment est le bord de la nappe. Comme on n'a pas inclus les valeur 0 et 1 dans le domaine de définition de l'application
: ces lignes sont les lignes extrémités de la nappe, on dit que l'ensemble qu'elles forment est le bord de la nappe. Comme on n'a pas inclus les valeur 0 et 1 dans le domaine de définition de l'application 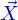 , ces lignes sont obtenues par un passage aux limites (comme pour les lignes).
, ces lignes sont obtenues par un passage aux limites (comme pour les lignes).
-
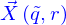 : cette ligne est la ligne décrite par la variable
: cette ligne est la ligne décrite par la variable  lorsque la variable
lorsque la variable
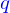 est fixée à la valeur constante
est fixée à la valeur constante  .
.
-
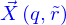 : idem en changeant les
: idem en changeant les 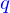 en
en  et vice-versa.
et vice-versa.
L'ensemble des lignes 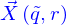 obtenues lorsqu'on fait varier
obtenues lorsqu'on fait varier 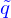 entre 0 et 1 forme ce qu'on appelle une famille de courbes. Mais l'ensemble contient aussi les points de la nappe.
entre 0 et 1 forme ce qu'on appelle une famille de courbes. Mais l'ensemble contient aussi les points de la nappe.
On peut faire, mutatis mutandis, le même commentaire pour les lignes 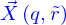 .
.
Et donc la nappe peut être vue comme une famille de courbes d'au moins deux façons. Mais il y a bien plus de familles de courbes que ces deux familles. On peut s'en convaincre en faisant un changement de variables sur les variables 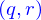 : soit on introduit une application
: soit on introduit une application
et on suppose que cette application est une bijection bicontinue (ou homéomorphisme) (l'inverse est continu). La nappe peut alors être définie par
et on voit que les deux familles de courbes qu'on peut former avec cette nouvelle application (dont les valeurs sont bien les points de la nappe initiale) sont différentes de celles qu'on avait avec l'ancienne.
C'est pour cette raison que, même si une nappe peut être vue comme une famille de courbe, en général on n'insiste pas sur cette interprétation. Mais c'est néanmoins une interprétation très utile. Notamment pour voir ce qu'est le plan tangent en un point de la nappe.
Pour la paramétrisation 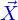 , un point de la nappe est repéré par une valeur de
, un point de la nappe est repéré par une valeur de 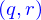 . Ce point est l'intersection des deux lignes :
. Ce point est l'intersection des deux lignes :  et
et  .
.
Les vecteurs tangents à chacune de ces lignes en ce point sont obtenus par dérivation de 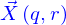 : pour la première, par rapport à
: pour la première, par rapport à  ; pour la seconde, par rapport à
; pour la seconde, par rapport à  . On les note
. On les note
On veut que ces vecteurs permettent de construire un plan tangent à la nappe en 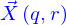 . Il est donc nécessaire que
. Il est donc nécessaire que
- Ils ne soient pas individuellement nuls, soit
si l'un d'eux l'était, la ligne dont il est la tangente ne serait pas bien définie.
- Ils ne soient pas alignés l'un sur l'autre, soit
Bien sûr cette condition entraîne celle qui la précède (si le produit vectoriel des deux vecteurs n'est pas nul, c'est qu'aucun des deux vecteurs n'est nul). Mais elle est plus forte qu'elle puisque les vecteurs peuvent ne pas être nuls alors que leur produit vectoriel l'est (lorsqu'ils sont colinéaires).
Avec ces conditions, on peut construire le vecteur normal à la nappe en 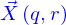 , c'est
, c'est
Ce vecteur est défini comme dépendant de la position 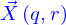 sur la nappe et non pas des
sur la nappe et non pas des 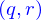 parce qu'il ne dépend pas de la paramétrisation utilisée. On peut faire un calcul (analogue à celui qui a été fait pour montrer que le vecteur tangent à une ligne ne dépend pas non plus de la paramétrisation de la ligne) pour le montrer, c'est laissé en exercice.
parce qu'il ne dépend pas de la paramétrisation utilisée. On peut faire un calcul (analogue à celui qui a été fait pour montrer que le vecteur tangent à une ligne ne dépend pas non plus de la paramétrisation de la ligne) pour le montrer, c'est laissé en exercice.
Description paramétrique du domaine
Comme pour les nappes on se limite à la représentation paramétrique des domaines. Le terme domaine a été utilisé pour « volume » qui sera réservé pour désigner la mesure d'une portion de domaine.
Dans cette représentation paramétrique, un domaine est l'image de l'intervalle 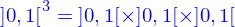 par une application
par une application
qui est donnée. La valeur de l'application peut être représentée par ses coordonnées cartésiennes où s'introduisent les fonctions coordonnées
Ces fonctions coordonnées, sont des fonctions à valeur réelle mais dépendant de trois variables réelles. Le traitement est analogue à celui des fonctions qui définissaient les nappes, en rajoutant juste une variable.
Le domaine peut être vu comme une famille de nappes : les nappes sont celles qui sont paramétrées par 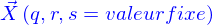 et le paramètre supplémentaire qui indexe les nappes dans la famille est
et le paramètre supplémentaire qui indexe les nappes dans la famille est 
Mais on peut aussi choisir les nappes 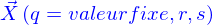 ou encore
ou encore 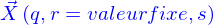
La condition pour que l'application 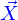 soit la paramétrisation d'un domaine est déjà que les éléments de ces familles soient vraiment des nappes. Et il faut aussi ajouter que le paramètre d'indexation des nappes dans une famille conduit bien à former des nappes différentes lorsqu'il varie.
soit la paramétrisation d'un domaine est déjà que les éléments de ces familles soient vraiment des nappes. Et il faut aussi ajouter que le paramètre d'indexation des nappes dans une famille conduit bien à former des nappes différentes lorsqu'il varie.
Pour cela il faut et il suffit que le produit mixte des trois vecteurs 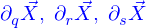 soit non nul, soit
soit non nul, soit
Suivant la complexité de la forme du domaine qu'il s'agit de décrire, le produit mixte en un point de ce domaine peut prendre toute une série de valeurs mais il ne doit jamais s'annuler.
On convient en général de choisir la paramétrisation pour qu'il soit positif. Ce qui revient, au cas où on aurait une paramétrisation où il est négatif, à choisir l'un quelconque des couples de 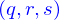 .
.
Lieux : description implicite
Les lieux ont été définis paramétriquement. Mais ils peuvent aussi l'être par des conditions portant sur les coordonnées. Appelons cela une définition implicite.
Si on donne une fonction
l'équation
a pour solution un certain ensemble de triplets 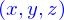 , on l'appelle
et on considère l'ensemble de points de
, on l'appelle
et on considère l'ensemble de points de 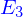
Suivant les propriétés dont on munit  et/ou l'expression qu'on lui donne, l'ensemble
et/ou l'expression qu'on lui donne, l'ensemble  peut être
peut être
- vide, e.g.
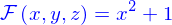
- limité un ou quelques points, e.g.
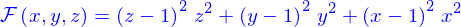
- Un nombre infini de points séparés les uns des autres, e.g.
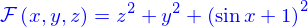
- Une ligne, e.g.
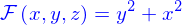
- Plusieurs lignes, e.g.
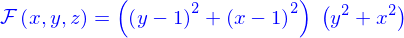
- Une nappe, e.g.
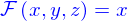
- Un domaine, e.g.
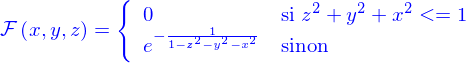
- Et bien d'autres choses encore...
Les fonctions données en exemple sont toutes différentiables et même indéfiniment différentiables. Donc la différentiabilité ne suffit pas pour obtenir le résultat que l'on souhaite : faire que  soit une nappe et rien d'autre.
soit une nappe et rien d'autre.
La condition à ajouter pour obtenir le résultat est que les dérivées partielles de 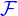 par rapport aux coordonnées
par rapport aux coordonnées  ne s'annulent pas toutes simultanément lorsque
ne s'annulent pas toutes simultanément lorsque 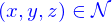
Cette condition, appelée la condition du théorème des fonction implicites est celle qui permet par exemple d'affirmer que
et donc de construire une paramétrisation de la nappe comme
On ne montre là que l'aspect suffisant de la condition et on admettra son aspect nécessaire.
Le gradient
Pour synthétiser ces résultats, le plus simple est encore d'introduire déjà la fonction
dont la définition est donnée par
On appelle gradient de 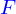 le vecteur dépendant de la position (on dira le champ de vecteurs plus loin) défini par
le vecteur dépendant de la position (on dira le champ de vecteurs plus loin) défini par
La définition implicite d'une nappe
Une nappe est alors définie comme
Un élément important de la nappe définie sous forme paramétrique était son vecteur normal en un point 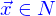 . Avec la définition implicite, ce vecteur normal d'exprime comme
. Avec la définition implicite, ce vecteur normal d'exprime comme
la démonstration est laissée en exercice.
La définition implicite d'une ligne
La définition implicite d'une ligne consiste à la représenter comme l'intersection de deux nappes définies elles-même implicitement.
On dispose d'une première nappe
on en ajoute une seconde
L'intersection des deux nappes forme un ensemble
Cet ensemble peut être
- Vide, e.g.
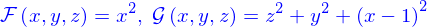
- Réduit à quelques points, e.g.
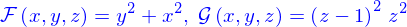
- Une ligne, e.g.
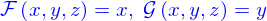
- Et d'autres lieux...
Pour obtenir une ligne, il faut que l'intersection des deux nappes ne soit pas vide et que le produit vectoriel des gradients de 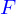 et
et  ne soit pas nul aux points d'intersection. Ce produit vectoriel permet de trouver le vecteur tangent aux points de la ligne, définis par
ne soit pas nul aux points d'intersection. Ce produit vectoriel permet de trouver le vecteur tangent aux points de la ligne, définis par
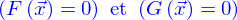
comme
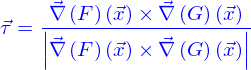
On aurait également pu choisir l'opposé de ce vecteur
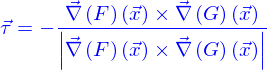
comme vecteur tangent. La définition de la ligne comme intersection de deux nappes ne dit rien de l'orientation de cette ligne, c'est laissé libre.
Description qualitative des domaines et leur connexité
Insuffisance de la description paramétrique
Un lieu  est dit borné si
est dit borné si
tous les points qui le composent sont situés à distance finie de l'origine.
On considère un domaine  borné défini paramétriquement à partir de l'application (différentiable)
borné défini paramétriquement à partir de l'application (différentiable)
comme l'image du pavet  par l'application
par l'application  , soit
, soit
Si le domaine est borné, l'application 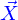 doit (je n'en suis pas sûr mais ça semble raisonnable) admettre une limite lorsque les
doit (je n'en suis pas sûr mais ça semble raisonnable) admettre une limite lorsque les 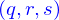 atteignent 0 ou 1.
atteignent 0 ou 1.
A priori, le bord du domaine  est l'ensemble
est l'ensemble
qui est formé des images par 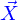 des 6 facettes du cube
des 6 facettes du cube  .
.
Chacune de ces facettes peut former une nappe ou non. Si par exemple
c'est le cas. Mais pas si Là, la facette  est le segment
est le segment 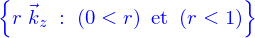 . De plus les facettes
. De plus les facettes  et
et  coïncident, c'est le rectangle
coïncident, c'est le rectangle 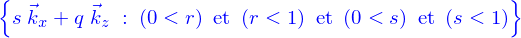 .
.
De plus, même le cas
où le domaine est un simple cube pose un problème. Le « bord » 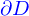 contient bien les facettes du cube mais pas ses arêtes. On peut toujours essayer de lui ajouter ces 12 arêtes, mais alors quelle serait le vecteur normal sur elles ?
contient bien les facettes du cube mais pas ses arêtes. On peut toujours essayer de lui ajouter ces 12 arêtes, mais alors quelle serait le vecteur normal sur elles ?
C'est ce genre de raisons qui limite l'intérêt de la définition paramétrique des domaines. Les voir comme l'image d'un pavet  ne permet pas d'identifier simplement leurs bords.
ne permet pas d'identifier simplement leurs bords.
Tentative de description qualitative d'un domaine et de son bord
Ce bord d'un domaine, par ailleurs, est assez clairement l'ensemble des points qui n'appartiennent pas au domaine mais qui ne lui sont pas non plus tout à fait extérieurs dans le sens qu'on peut trouver des points du domaine qui leur sont aussi proches qu'on le veut. Et de la même façon on peut trouver des points qui n'appartiennent ni au domaine ni à son bord qui sont aussi proches qu'on veut des points du bord.
Pour préciser cela il faudrait introduire des notions qui relèvent de la topologie ; ces notions permettent d'appréhender abstraitement ce qu'on a appelé les lieux (de points) et de fournir un cadre formel éclairant qui ne nécessite pas les calculs laborieux des définitions paramétriques qui ont été faites.
Ce serait trop long d'introduire ces notions. Par contre on peut introduire des éléments de langage plus ou tirés de ces notions qui permettent de décrire qualitativement des ensembles comme ceux des domaines.
Un domaine doit donc être perçu comme un ensemble de points tels que chacun de ces éléments est le centre d'une boule suffisamment petite pour que tous les points de la boule appartiennent au domaine.
Le bord 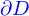 de ce domaine est l'ensemble des points tels que, si petite soit la boule qu'on forme avec ces points aux centres, celle-ci contiendra à la fois des points du domaine et des points qui ne lui appartiennent pas.
de ce domaine est l'ensemble des points tels que, si petite soit la boule qu'on forme avec ces points aux centres, celle-ci contiendra à la fois des points du domaine et des points qui ne lui appartiennent pas.
L'extérieur 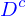 du domaine est l'ensemble des points qui n'appartiennent pas au domaine telsqu'on puisse toujours trouver une boule suffisamment petite pour que tous les points de la boule soient extérieurs au domaine.
du domaine est l'ensemble des points qui n'appartiennent pas au domaine telsqu'on puisse toujours trouver une boule suffisamment petite pour que tous les points de la boule soient extérieurs au domaine.
En s'aidant éventuellement d'un dessin
on peut se convaincre d'avoir compris ces définitions. Ce qu'est la boule n'a pas été défini mais on en a une idée intuitive ; moins intuitivement c'est l'ensemble des points qui sont à distances (euclidienne) d'un point qui est son centre plus petites qu'un certain rayon qu'on se donne, en plus du centre, pour caractériser cette boule.
Connexité et simple connexité des domaines
Les domaines ainsi conçus, ont des degrés de complexité. Ces degrés sont qualifiés par la notion de connexité.
Un domaine est connexe s'il est d'un seul tenant. Ou encore s'il est possible de joindre deux points quelconques du domaine par une ligne telle que chacun des points du domaine sont intérieurs à ce domaine.
Un domaine non connexe est composé de parties qui sont elles connexes et qu'on appelle ses composantes connexes. Il est possible de concevoir un domaine qui a un nombre infini de composantes connexes mais soit ce domaine n'est pas borné, soit certaines de ses composantes connexes deviennent si petites qu'on ne peut plus trop les assimiler à des domaines connexes. Mais laissons là ce genre de subtilité.
Un domaine connexe est dit simplement connexe s'il ne comporte pas de trous intérieurs (penser à l'enveloppe d'un ballon) et qu'il ne comporte pas de boucles. Pour voir ce qu'est une boucle, il suffit de considérer le tore
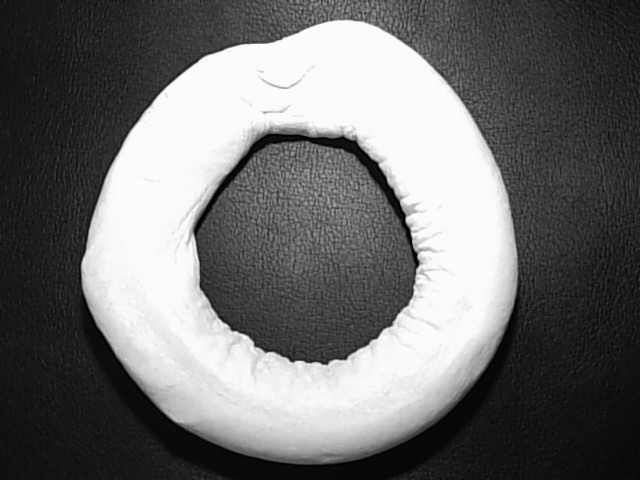
mais ça peut être encore plus complexe, comme le nœud
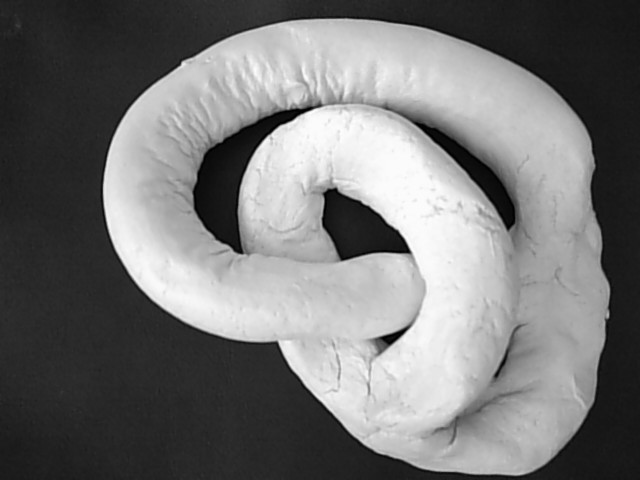
ou encore le bretzel
Si on veut disposer d'un moyen de caractériser un domaine simplement connexe, on peut le voir comme un domaine tel qu'une ligne fermée sur elle même (  ) puisse être déformée par petites étapes (on dit continûment) jusqu'à pouvoir être réduite à un seul point sans jamais que les points qui la composent cessent d'être des points du domaine. Mais cela suppose de définir ce qu'on a appellé une déformation, ce qui nous emmènerait trop loin.
) puisse être déformée par petites étapes (on dit continûment) jusqu'à pouvoir être réduite à un seul point sans jamais que les points qui la composent cessent d'être des points du domaine. Mais cela suppose de définir ce qu'on a appellé une déformation, ce qui nous emmènerait trop loin.
Description implicite des domaines
On n'a pas jusqu'ici cherché à donner une définition implicite des domaines dans la section éponyme parce qu'il faut pour cela disposer des notions de connexité et surtout simple connexités qui sont expliquée dans la sous-section précédente.
On a également vu, toujours sans la sous-section précédente et sur le cas du cube, que ce qu'on pourrait raisonnablement assimiler au bord d'un domaine à quelque chose qui ressemble à une nappe mais n'en est cependant pas tout à fait.
Il est donc nécessaire d'élargir la définition de la nappe pour qu'un bord de domaine puisse être un nappe.
Description qualitative des nappes
Une nappe peut être vue comme un ensemble de positions tels que, pour chacune d'entre elles on puisse trouver une boule dont il est le centre et suffisamment petite pour que les points qu'elle contient forment deux ensembles disjoints et séparés par les positions de la nappe.
Le dessin montre en traits pleins la demi boule supérieure qui contient des points situés d'un côté de la nappe. Il y a aussi la demi boule inférieure qui contient les points situés de l'autre coté représentée en pointillés.
Les nappes ainsi conçues ont, comme les domaines, des degrés de complexités qui peuvent déjà être appréhendé au moyen des notions de connexité et simple connexité.
Comme donc pour un domaine, une nappe est connexe si elle est d'un seul tenant. Il est possible de joindre deux quelconques de ses points par une ligne dont tous les points appartiennent à la nappe.
La nappe est simplement connexe s'il est possible de réduire, par déformation continue (cette déformation n'est pas plus définie qu'elle ne l'a été pour les domaines, on est prié de s'en faire une idée par soi-même), une ligne fermée sur elle même et tracée sur la nappe à un point de la nappe.
Un nappe qui n'est pas simplement connexe est une nappe qui comporte un ou plusieurs trous.
Les nappes ont aussi une dimension de complexité en dehors de la connexité. C'est celle de l'orientabilité. Celle-ci se comprend bien avec l'exemple ruban de Moebius
.
Si on dessine une ligne continue de "+" sur le ruban
on remarque que celle-ci forme une ligne continue qui s'étend des deux côtés de la feuille de papier qu'on a utilisé pour fabriquer le ruban.
Si on plante des épingles au centre des "+", toujours dans le même sens et en les plaçant une par une, on arrive à ce que la dernière épingle avant de revenir à la première plantée se retrouve orienté en sens inverse de cette première épingle
Les épingles figurent les vecteurs normaux à la nappe. La petite expérimentation menée avec ces épingles fait voir qu'il n'est pas possible de munir chacun des points du ruban de Moebius d'un vecteur normal de façon que les vecteurs normaux de deux points voisins soient approximativement les mêmes.
Si on essaie de le faire on trouvera toujours un endroit où deux points voisins du ruban ont des vecteur normaux de sens opposé.
Une nappe qui recèle cette caractéristique est dite non-orientable. Et orientable si elle ne l'a pas.
Le bord des lignes, nappes et domaines
Il reste finalement une dernière notion à préciser. Qu'on a d'ailleurs déjà utilisé pour les lignes quand on a invoqué les lignes fermées sur elles même.
La ligne fermée sur elle même correspond à un élastique bracelet
Si elle n'est pas fermée sur elle même, elle comporte deux extrémités, on peut appeler celles ci le bord de la ligne. À partir d'une de ces extrémités, on peut se déplacer le long de la ligne d'un côté mais pas de l'autre.
Il y a aussi des nappes fermées sur elles même, par exemple la sphère, sous forme implicite
Lorsque la nappe n'est pas fermée sur elle même, ses extrémités forment une ligne, qu'on peut appeler son bord. Même une surface... disons excentrique a un bord, On peut examiner celui d'un ruban de Moebius en coupant celui-ci le long de la ligne où on a dessiné les croix, cela donne
c'est encore une sorte de ruban qui n'est sans doute pas orientable (à vérifier). Si on coupe de la même façon (le long d'une ligne au centre du ruban) ce ruban, on obtient
C'est deux rubans distincts imbriqués. Si on les suppose de largeur suffisamment petite pour être assimilés à des lignes, on obtient que le bord d'un ruban obtenu par découpe d'un ruban de Moebius est la réunion de deux lignes, c'est un ensemble non connexe.
Ce ne sont pas des choses simples. Mais heureusement on ne va pas à chercher à étudier cela précisémment, c'est à dire en introduisant les notions mathématiques qui permettent cette précision.
Par contre, ces petites expérimentation avec une bande de papier amènent à comprendre au moins intuitivement, ce qu'est le bord d'une nappe. C'est un ensemble (non nécessairement connexe) de lignes.
Si maintenant on revient au cas où la nappe n'a pas de bord (la sphère), on se rend compte qu'elle délimite tout l'espace en deux parties. Comme on l'a vu précédemment, pour toute nappe (y compris celles qui ont un bord) et pout tout point de cette nappe, il est possible de trouver une boule centrée sur lui et suffisamment petite pour que qu'une partie des points de la nappe soit située localement d'un côté de la nappe alors que les autres sont situés de l'autre côté. Mais quand la surface n'a pas de bord, cette propriété locale devient globale.
C'est à dire qu'un nappe sans bord (ou fermée sur elle-même) sépare l'espace en deux partie : l'une est d'un côté de la nappe et l'autre est de l'autre côté.
Description implicite des domaines
Cette dernière affirmation permet la définition d'un domaine comme l'ensemble des points qui sont situés d'un seul côté d'une nappe fermée ; cette nappe étant le bord du domaine.
C'est une définition implicite si la nappe est donnée sous forme implicite. Par exemple la boule centrée sur l'origine et de rayon  est
est
Lorsqu'on définit ainsi un domaine, on prend systématiquement la convention d'orienter les vecteurs normaux en chacun des points de son bord vers l'extérieur du domaine.
Mais, à ce propos, il reste encore à ajouter que, par exemple dans le cas du cube dont le bord est l'ensemble des facettes de ce cube (auxquelles on ajoute les arêtes), il est possible que certaines lignes tracées sur ce bord n'aient pas de vecteurs nomraux bien définis.
Dans ce cas on convient de ne pas s'inquiéter de cela avec l'argument (qui pourait être précisé mathématiquement) qu'un nombre fini de lignes sur une nappe correspond à un ensemble de points assez rares par rapport à ceux qui ne sont pas sur la ligne. On dit que les vecteurs normaux sont définis presque partout (et on suppose que le fait qu'ils ne le soit pas partout ne gène en rien pour ce qu'on a à faire avec le domaine).
Symétries
Les objets à 3 dimensions d'espace sont représentés par des domaines (pour reprendre la terminologie de Newton : un corps solide est un morceau d'espace qu'une cause première a voulu impénétrable). Ces objets peuvent avoir des symétries dont il est utile de répertorier les plus courantes.
Symétrie cylindrique
La première de ces symétries usuelles est la symétrie cylindrique : elle traduit l'invariance d'un domaine dans une direction fixe. Pour un domaine défini implicitement, une forme générale est
où  est un point de l'espace et
est un point de l'espace et 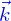 un vecteur tel que
un vecteur tel que 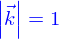 quelconque.
quelconque.
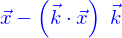 est la projection de
est la projection de 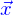 dans le plan passant par l'origine et normal à
dans le plan passant par l'origine et normal à 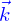 ; et on peut dire la même chose en remplaçant
; et on peut dire la même chose en remplaçant 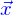 par
par  à ceci près que le vecteur projeté est
à ceci près que le vecteur projeté est 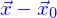 et que le plan passe par
et que le plan passe par 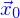 .
.
Par exemple avec
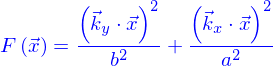
et
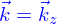
on obtient un cylindre dont la base est une ellipse (un cercle pour 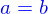 ).
).
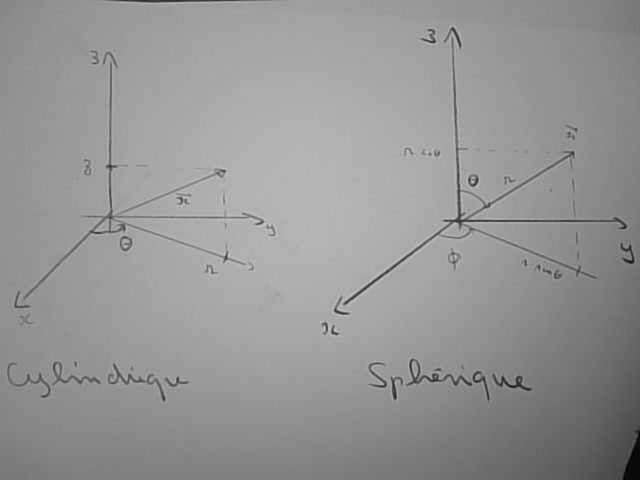
Symétrie axisymétrique
La seconde des symétries usuelles est la symétrie axisymétrique : elle traduit l'invariance d'un domaine par rotation autour d'un axe.
On la définit facilement en utilisant les coordonnées cylindriques. Pour les obtenir, on pose
et inversement
Un vecteur  peut alors s'écrire
peut alors s'écrire
La position est donc spécifiée par trois nombres :  qui s'appellent les coordonnées cylindriques de
qui s'appellent les coordonnées cylindriques de 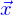 .
.
L'application de passage des coordonnées cylindriques aux coordonnées cartésiennes
où l'axe z est l'ensemble des positions repérées par  . Cet axe est exclu de l'ensemble d'arrivée parce que la valeur
. Cet axe est exclu de l'ensemble d'arrivée parce que la valeur  est exclue de l'ensemble de départ. L'application est continue et différentiable (indéfiniment) et bijective sur les ensemble de départ et d'arrivée spécifiés. Son inverse (également différentiable) peut être construit avec
est exclue de l'ensemble de départ. L'application est continue et différentiable (indéfiniment) et bijective sur les ensemble de départ et d'arrivée spécifiés. Son inverse (également différentiable) peut être construit avec
Ceci étant rappelé, la symétrie axisymétrique d'axe l'axe passant par l'origine et de direction  correspond à
correspond à
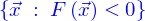
pour
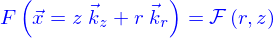
Symétrie de rotation (isotropie)
La symétrie par une rotation d'axe quelconque passant par l'origine et la troisième symétrie usuelle. C'est celle de la sphère.
Les coordonnées adaptées pour la décrire sont les coordonnées sphériques. On pose
Ce qui s'inverse en
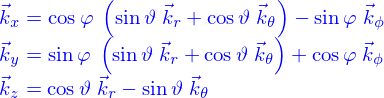
Un vecteur 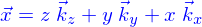 peut alors s'écrire
peut alors s'écrire
La position est donc spécifiée par trois nombres : 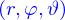 qui s'appellent les coordonnées sphériques de
qui s'appellent les coordonnées sphériques de  .
.
L'application de passage des coordonnées sphériques aux coordonnées cartésiennes est
Cette application est est continue et différentiable (indéfiniment) et bijective sur les ensemble de départ et d'arrivée spécifiés. Son inverse (également différentiable) peut être construit comme pour les coordonnées cylindriques. Il n'y a pas de difficulté pour trouver
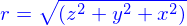
; l'angle

se trouve avec la même formule que pour le
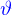
des coordonnées cylindriques ; et l'angle
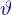
par une formule analogue quoique plus simple puisque
.
Ces formules peuvent paraître compliquées mais un dessin permet de les rendre plus intelligibles, par exemple
Ce que peut représenter un champ de scalaires
Un champ de scalaire est une application
où  est un domaine. La dépendance en
est un domaine. La dépendance en  est à comprendre comme celle de la fonction
est à comprendre comme celle de la fonction  vis-à-vis de la fonction
vis-à-vis de la fonction 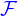 utilisée pour la définition implicite des nappes, soit
utilisée pour la définition implicite des nappes, soit
Les champs de scalaires peuvent représenter
- des potentiels, e.g. le potentiel gravitationnel
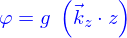 à partir duquel le champ de pesanteur est
à partir duquel le champ de pesanteur est 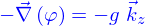 ;
;
- des densités de quantité, e.g. la concentration en sel dans un domaine
 qui représente un certain volume d'eau.
qui représente un certain volume d'eau.
On va constamment utiliser la dénotation de densité de quantité pour étudier les champs scalaires. Parce qu'il sera toujours possible de rattacher les expressions mathématiques à une interprétation physique bien plus simple que celles qui correspondent aux potentiels.
Aussi, évite-t'on de nommer ces potentiels avec des lettres comme  mais on va plutôt utiliser
mais on va plutôt utiliser  , soit
, soit
pour utiliser une notation usuelle.
Prêter à  la dénotation d'être une densité de quantité, suppose qu'on introduise déjà la quantité dont elle est la densité. Cette quantité peut être n'importe quelle variable extensive au sens de la thermodynamique : la masse, le volume (et aussi la longueur et la surface), l'énergie, la quantité de sel,...
la dénotation d'être une densité de quantité, suppose qu'on introduise déjà la quantité dont elle est la densité. Cette quantité peut être n'importe quelle variable extensive au sens de la thermodynamique : la masse, le volume (et aussi la longueur et la surface), l'énergie, la quantité de sel,...
Comment former des quantités à partir de leurs densités
La densité de quantité est une représentation du fait que les quantités sont réparties dans l'espace.
Il est donc nécessaire avant toute autre chose de disposer d'un moyen de quelle quantité contient tel ou tel autre domaine de l'espace.
Supposons que le domaine dont il s'agit soit un petit cube  défini paramétriquement par
défini paramétriquement par
Si 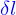 est très petit, la valeur de
est très petit, la valeur de  (supposée continue) ne varie pas beaucoup dans le cube, et donc la quantité que ce cube contient est
(supposée continue) ne varie pas beaucoup dans le cube, et donc la quantité que ce cube contient est
Si donc le domaine  peut être pavé par de tels petits cubes, on peut obtenir la quantité contenue par
peut être pavé par de tels petits cubes, on peut obtenir la quantité contenue par  en sommant toutes les contributions des petits cubes formés en faisant varier
en sommant toutes les contributions des petits cubes formés en faisant varier 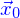 .
.
C'est le principe de l'intégration de Riemann mais il y a là une difficulté supplémentaire : comment remplir un domaine quelconque avec de tels petits cubes ?
Si le domaine  est défini paramétriquement comme l'image de l'intervalle
est défini paramétriquement comme l'image de l'intervalle 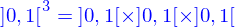 par une application
par une application
on peut introduire des petits cubes dans 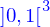 , par exemple
avec
où les
, par exemple
avec
où les 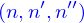 sont des entiers allant de
sont des entiers allant de 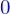 à
à  et où
et où  est un nombre entier qui peut être choisi aussi grand qu'on veut pour que les cubes
est un nombre entier qui peut être choisi aussi grand qu'on veut pour que les cubes 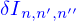 soient aussi petits qu'on veut.
soient aussi petits qu'on veut.
L'image d'un 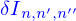 par l'application
par l'application 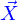 n'est pas un cube. Mais si
n'est pas un cube. Mais si  est très grand,
est très grand, 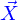 varie suffisamment peu pour qu'on puisse approximer l'image des arêtes du cube
varie suffisamment peu pour qu'on puisse approximer l'image des arêtes du cube 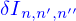 par des segments droits. On obtient donc que cette image est un parallépipède de base les
par des segments droits. On obtient donc que cette image est un parallépipède de base les
et donc de volume leur produit mixte
D'autre part, si le parallélépipède est très petit, la densité  ne varie pas sensiblement sur toute son étendue, et donc la contribution de l'image par
ne varie pas sensiblement sur toute son étendue, et donc la contribution de l'image par 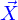 du petit cube
du petit cube 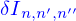 à la quantité cherchée est
à la quantité cherchée est
Pour obtenir toute la quantité contenue dans le domaine  , il suffit de sommer sur tout les cubes
, il suffit de sommer sur tout les cubes 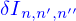 pour obtenir
pour obtenir
Et finalement le passage à la limite, fournit la quantité
Et c'est ce que qu'on note
avec
où 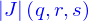 est appelé le jacobien de l'application
est appelé le jacobien de l'application 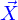 .
.
Si on on connaît des primitives des intégrales successives de 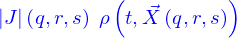 on peut calculer la quantité
on peut calculer la quantité  .
.
Si on ne les connaît pas, il faut utiliser le calcul numérique. Comme d'ailleurs si la forme du domaine est donnée implicitement et qu'on ne trouve pas de paramétrisation correspondante.
Mais la question du calcul pratique est moins importante ici que la compréhension de ce que signifie
c'est une notation synthétique pour l'expression comportant une intégrale triple.
Flux advectif de densités
On donne dans tout l'espace 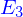 un champ de vitesses eulérien
un champ de vitesses eulérien
Il y a aussi, toujours dans  une quantité qui est répartie avec la densité
une quantité qui est répartie avec la densité 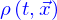 .
.
Pour donner une dénotation claire à ce qui suit, la densité dont il s'agit est un nombre de particules par unité de volume.
Le champ de vitesse a pour action transporter les particules au cours du temps ; on suppose qu'elle le sont de façon que si une particule est en 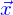 à l'instant
à l'instant  , elle se retrouvera en
, elle se retrouvera en 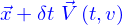 à l'instant
à l'instant 
La question est de savoir combien de particules traversent la nappe  décrite paramétriquement par
décrite paramétriquement par 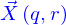 entre les instants
entre les instants  et
et  , étant petit
, étant petit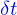
Pour cela, on découpe cette nappe en petits morceaux comme
et on s'intéresse déjà à la question de savoir combien de particules traversent le morceau en rouge qui est décrit par 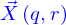 pour
pour 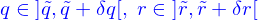 ,
, 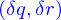 étant petits.
étant petits.
Ce morceau n'est pas un parallélogramme, mais si 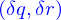 sont effectivement petits l'approximation pour laquelle il l'est est acceptable. On la fait. Cela permet déjà d'affirmer que sa contribution à la surface de la nappe est
sont effectivement petits l'approximation pour laquelle il l'est est acceptable. On la fait. Cela permet déjà d'affirmer que sa contribution à la surface de la nappe est
d'où vient, par un procédé de passage à la limite comme celui qui a été explicité à la sous-section précédente pour le volume, que la surface de la nappe est
Si le parallélogramme est petit, on peut tout aussi bien considérer que le champ de vitesses est uniforme sur les points qui le composent. Ainsi d'ailleurs que la densité 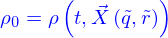 . Cela rend possible le calcul du nombre de particules qui traversent le parallélogramme.
. Cela rend possible le calcul du nombre de particules qui traversent le parallélogramme.
Le champ de vitesses sur le parallélogramme est 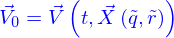 , il s'exprime à partir du vecteur
, il s'exprime à partir du vecteur  normal à ce parallélogramme comme
normal à ce parallélogramme comme
où 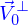 est la projection du vecteur
est la projection du vecteur 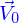 sur le plan du parallélogramme.
sur le plan du parallélogramme.
On peut alors voir que les particules qui traversent le parallélogramme pendant le laps de temps  sont celle qui sont situées dans le volume situé en dessous (par rapport à la direction du vecteur
sont celle qui sont situées dans le volume situé en dessous (par rapport à la direction du vecteur 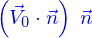 ) de celui-ci et de profondeur
) de celui-ci et de profondeur 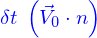
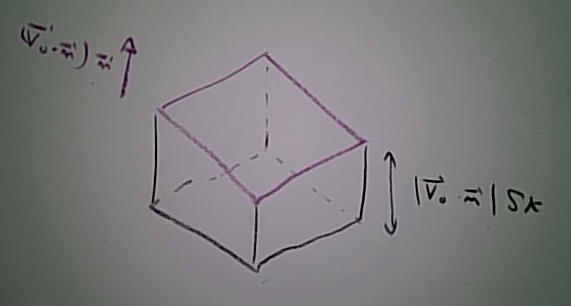
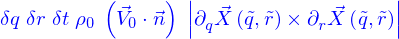
(Les particules sont également entraînées par  , mais c'est dans le sens du plan tangent au parallélograme et donc ça ne contribue pas au nombre de particules qui le traversent.)
, mais c'est dans le sens du plan tangent au parallélograme et donc ça ne contribue pas au nombre de particules qui le traversent.)
Si on somme les contributions de tous les parallélogrammes, on obtient (par un passage à la limite) le nombre 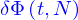 de particules qui traversent la nappe à l'instant
de particules qui traversent la nappe à l'instant  pendant le laps de temps
pendant le laps de temps 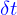 . C'est
. C'est
en convenant que
soit, encore et puisque
La forme que prend 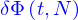 , porte à considérer la densité de flux advectif de particules
, porte à considérer la densité de flux advectif de particules
qui a pour unité le nombre de particules par
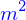
et par

On peut ainsi introduire
qui s'appelle le flux advectif de particules : c'est le nombre de particules qui traversent

par seconde, ou encore le débit de particules. À partir de ce flux advectif on obtient le nombre de particules qui traversent

de

à

par
Pour finir, jusqu'ici on a particularisé la densité en une densité de particules (ou concentration en nombre) pour des raisons pédagogiques. Mais tout ce qui a été établi reste valable pour toute densité représentant la répartition dans l'espace de n'importe quelle quantité extensive.
Et donc il est possible d'oublier la dénotation de cette densité en nombre de particule par unité de volume en conservant les résultats.
Flux conductif de densités
Le flux advectif était dû à la présence d'un champ de vitesses qui déplacait les quantités.
Le flux conductif a une origine à la fois similaire, les particules ne pouvant guère se déplacer sans avoir une vitesse, et différente : d'une part le champ de vitesses qui déplace les particules est une variable aléatoire et d'autre part on ne considère plus tant les particules individuellement qu'en moyenne.
L'explication de cette remarque (qu'on peut juger à juste titre sibylline) relève de la physique et il n'est pas dans l'intention de cet enseignement d'en faire. On se limite en gros à traiter de la configuration et de la cinématique des systèmes.
Aussi va-t'on admettre que le mécanisme de conduction correspond à ce que la densité de flux de particules est
et cela sans qu'il y ait de champ de vitesses.
 est appelé la diffusivité (en
est appelé la diffusivité (en  ; c'est une constante positive caractéristique du type de densité à laquelle on associe un mécanisme de conduction.
; c'est une constante positive caractéristique du type de densité à laquelle on associe un mécanisme de conduction.
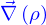 est le gradient de
est le gradient de  . On a déjà vu ce qu'était un gradient lorsqu'on a représenté implicitement une nappe. Ce gradient a exactement la même expression. Soit, si (on utilise le même symbole
. On a déjà vu ce qu'était un gradient lorsqu'on a représenté implicitement une nappe. Ce gradient a exactement la même expression. Soit, si (on utilise le même symbole  à gauche et à droite pour éviter d'alourdir)
à gauche et à droite pour éviter d'alourdir)
et on ne met pas les arguments des dérivées partielles de  mais ceux-ci sont
mais ceux-ci sont 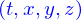 .
.
La densité de flux conductif ainsi définie a exactement la même signification que la densité de flux advectif. Si on donne une nappe  , que la densité est une densité de particules, le nombre de particules qui traversent la nappe par unité de temps (son flux ou encore débit) est
, que la densité est une densité de particules, le nombre de particules qui traversent la nappe par unité de temps (son flux ou encore débit) est
Équations d'advection, de diffusion et d'advection-diffusion
On a obtenu que la quantité répartie dans le domaine  avec la densité
avec la densité  était
était
Le flux  de cette quantité à travers le bord
de cette quantité à travers le bord 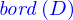 de ce domaine est
de ce domaine est
C'est aussi (par la formule de Green-Ostrogradki)
En reprenant l'image des particules, c'est le nombre des particules qui quittent le domaine  par unité de temps. Mais ce nombre est aussi
par unité de temps. Mais ce nombre est aussi
le signe "-" parce qu'avec le signe "+" ce serait le nombre de particles qui arrivent dans le domaine par unité de temps.
Il vient donc
et ça doit être valable pour tout domaine, y compris pour un domaine très petit autour d'un point quelconque. Il faut donc qu'en tout point
Si le mécanisme créant le flux est l'advection sous l'action d'un champ de vitesses  alors
alors 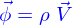 et
et
c'est l'équation d'advection.
Si c'est la diffusion alors 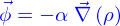 où
où  est la diffusivité et
est la diffusivité et
c'est l'équation de diffusion.
Et si les deux effets sont combinés, 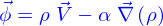 on obtient
on obtient
qui est l'équation d'advection-diffusion.
Équations aux dérivées partielles
Une équation aux dérivées partielles (EDP) est une relation algébrique entre un champ  et ses dérivées partielles. Par exemple
et ses dérivées partielles. Par exemple
celle-ci n'est ni linéaire ni même correctement dimensionnée (si  est un temps et
est un temps et 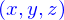 des distances). On ne s'occupera pas de tels formes.
des distances). On ne s'occupera pas de tels formes.
Une EDP linéaire est une relation linéaire entre le champ et ses dérivées partielles. On classe les EDP linéaire par le degré maximum de dérivation du champ qu'elle contient.
Une EDP linéaire de degré 1 est de la forme
ses coefficients peuvent dépendre du temps et de la position.
Une EDP linéaire de degré 1 à coefficients constants est de la forme
les coefficients sont des constantes.
On va maintenant cesser de reporter systématiquement la dépendance en 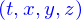 pour que les expressions soient plus lisibles.
pour que les expressions soient plus lisibles.
Une EDP linéaire de degré 1 (à coefficients constants ou non) avec un second membre est de la forme
où le second membre est  ; il peut dépendre de
; il peut dépendre de 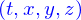 .
.
Une EDP linéaire du second ordre est de la forme (lire comme des produits de matrices de lignes ou colonnes 1)
Si elle a un second membre 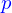 l'égalité se fait avec ce
l'égalité se fait avec ce 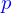 plutôt que 0.
plutôt que 0.
On voit donc que même en se limitant aux EDP de second ordre linéaires et avec second membre, il y a de la variété ! Celles qui sont utiles pour la physique sont cependant répertoriées et c'est de celles-ci qu'on traite.
Équation de Laplace
L'équation de Laplace est
Si elle a lieu dans tout l'espace, ses solutions sont appelées les fonctions harmoniques. On peut les construire assez facilement à partir d'expressions polynomiales classées par degrés, du moins jusqu'au degré 2
- degré 0, il y en a une
- degré 1, il y en a trois
- degré 2, il y en a cinq
après ça devient fatidieux. Et c'est au moins une des raisons qui poussent à faire ce genre d'études en coordonnées sphériques.
Cela suppose cependant de savoir écrire le laplacien dans ces coordonnées sphériques. C'est à dire que si (on laisse tomber la dépendance en temps)
Exercices
- Montrer que la longueur d'une ligne représentée par
est
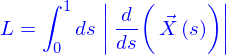
- Calculer la longueur d'une spire d'hélice, la spire d'hélice étant définie par
- Lorsqu'on tire sur un ressort hélicoïdal qui initialement est composé de
 spires d'hélice de rayon et pas
spires d'hélice de rayon et pas  , le rayon diminue et le pas s'allonge sans que la longueur de l'hélice par laquelle on représente le ressort ne change. On allonge donc le ressort de
, le rayon diminue et le pas s'allonge sans que la longueur de l'hélice par laquelle on représente le ressort ne change. On allonge donc le ressort de 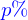 de sa longueur initiale, quelle est la variation de rayon ?
de sa longueur initiale, quelle est la variation de rayon ?
- Calculer le volume d'un ellipsoïde
On cherchera une paramétrisation adaptée.
- On donne une nappe définie implicitement par (
 )
)
- Trouver le vecteur normal en chacun des points de la nappe.
- Réécrire l'équation de la nappe en coordonnées cylindriques. Identifier ce qu'est la nappe.
- Trouver une paramétrisation de la nappe. Et vérifier que le vecteur normal qu'on peut calculer avec cette paramétrisation est le même qu'en a.
- On considère un tronçon de cylindre à section circulaire (hauteur
 , rayon
, rayon  ) qui forme un domaine
) qui forme un domaine 
- Écrire une paramétrisation de D
- Donner sous forme d'une paramétrisation
 , le bord de
, le bord de  et donner son champ de normales (orienté vers l'extérieur du domaine)
et donner son champ de normales (orienté vers l'extérieur du domaine) 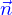
- Calculer le volume du domaine et la surface de son bord en utilisant les paramétrisations précédentes.
- Soit le champ de vecteurs
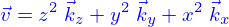 , calculer
, calculer 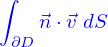
- directement ;
- En utilisant la formule de Green-Ostrogradski
- Trouver l'expression de la divergence en coordonnées cylindriques en exprimant la formule de Green-Ostrogradski sur le petit domaine
- Équation de propagation.
- On donne une fonction quelconque
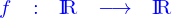 , dérivable deux fois. Montrer que
, dérivable deux fois. Montrer que 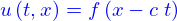 est solution de
est solution de
- Construire une solution de
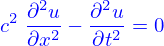 telle que
où
telle que
où 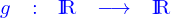 est une fonction quelconque.
est une fonction quelconque.
- Chercher la solution de
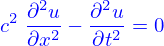 telle que
telle que
- Montrer que
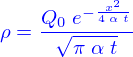 est solution de
En déduire une loi de progression de
est solution de
En déduire une loi de progression de 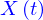 défini par
défini par 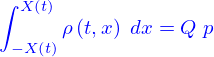 où
où 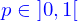
- Diffusion de sel dans de l'eau.
On place du sel au fond d’une éprouvette de rayon
 qu’on remplit d’eau pure jusqu’`a une hauteur
qu’on remplit d’eau pure jusqu’`a une hauteur 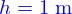 comptée à partir de l’interface sel/eau.
comptée à partir de l’interface sel/eau.
Le modèle qui permet de calculer l'évolution de la concentration de sel dans l'eau est celui de la diffusion. Ici la concentration est une fonction
qui est solution de
 où
où  est la coordonnée dans la direction de l'axe de l'éprouvette (
est la coordonnée dans la direction de l'axe de l'éprouvette ( 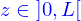 et
et ![]() le temps.
le temps.
Initialement l'eau est pure, donc 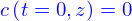 .
.
On fait l'hypothèse que 
et on suppose qu'au contact eau sel, la concentration est la concentration maximale du sel dans l'eau, soit  .
.
- Chercher la solution sous la forme
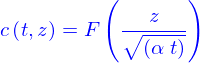 où
où  est une fonction à déterminer.
est une fonction à déterminer.
- On définit le flux de sel en
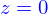 comme la quantité
comme la quantité 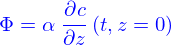 (c'est la quantité de sel qui entre dans l'eau par unité de surface de la section de l'éprouvette. Calculer
(c'est la quantité de sel qui entre dans l'eau par unité de surface de la section de l'éprouvette. Calculer 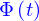 . Que se passe-t'il en
. Que se passe-t'il en 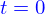 ?
?
- On définit la quantité de sel dans l'eau (par unité de surface) comme
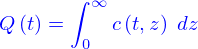 . Calculer
. Calculer 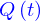
- Quelle est la relation entre
 et
et 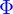 ?
?
- On appelle front de propagation du sel dans l'eau, la position
![]() telle que
telle que 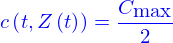 . Suivant quelle loi
. Suivant quelle loi  dépend-t'il du temps ?
dépend-t'il du temps ?
- On donne le problème
avec
et
où
 est un fonction donnée.
est un fonction donnée.
- Écrire l'équation différentielle ordinaire (EDO) et ses conditions aux limites dont la transformée de Laplace de
 (notée
(notée  ) est solution.
) est solution.
- Résoudre cette EDO et exprimer
 en fonction de
en fonction de  (la transformée de Laplace de
(la transformée de Laplace de  )
)
- Dans le cas où
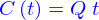 , donner l'expression de
, donner l'expression de 
- Même question pour

- Pour
 fonction quelconque, trouver une relation entre
fonction quelconque, trouver une relation entre  ,
, 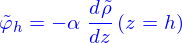 et
et 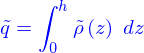
- On reprend le problème
mais avec des conditions initiales périodiques (elle ne sont plus vraiment initiales)
et une condition aux limites de la forme
- Montrer que
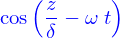 dès lors que
dès lors que  prend une valeur à préciser.
prend une valeur à préciser.
- Est-ce encore vrai pour
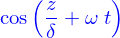 ,
, 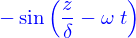 et
et 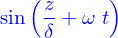 ?
?
- Si ça l'est, on dispose de 4 solutions de base qui permettent de construire la solution au problème proposé. Le faire.
 . Aussi l'espace ponctuel est-il assimilé à l'espace vectoriel. Et c'est cet espace vectoriel qui est utilisé pour représenter l'espace sensible.
. Aussi l'espace ponctuel est-il assimilé à l'espace vectoriel. Et c'est cet espace vectoriel qui est utilisé pour représenter l'espace sensible. ; on le note avec une flèche surlignante
; on le note avec une flèche surlignante 
 à partir de la définition de
à partir de la définition de  , appelons là
, appelons là 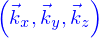 et alors les vecteurs de
et alors les vecteurs de 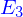 sont de la forme
sont de la forme 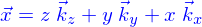 où
où 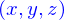 sont appelées les coordonnées cartésiennes du vecteur
sont appelées les coordonnées cartésiennes du vecteur 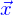
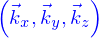 est orthonormée signifie que leurs produits scalaires sont tels que
est orthonormée signifie que leurs produits scalaires sont tels que

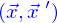 est
est


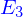 est l'espace des positions, l'unité physique de ses éléments est le mètre. Il serait donc cohérent de faire porter cette unité par les vecteurs de base, les coordonnées étant des nombres sans dimension qui fixeraient la quantité d'unité de longueur portée par les vecteurs de base.
est l'espace des positions, l'unité physique de ses éléments est le mètre. Il serait donc cohérent de faire porter cette unité par les vecteurs de base, les coordonnées étant des nombres sans dimension qui fixeraient la quantité d'unité de longueur portée par les vecteurs de base. 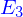 .
. 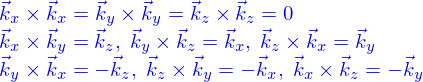
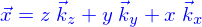 et
et  peut se calculer simplement à partir du
peut se calculer simplement à partir du 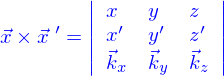
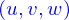 est une permutation paire des
est une permutation paire des 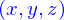 , le produit mixte
, le produit mixte 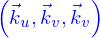 vaut 1 ; si c'est une permutation impair, il vaut -1 ; et si deux quelconques de ces vecteurs sont égaux, il vaut 0.
vaut 1 ; si c'est une permutation impair, il vaut -1 ; et si deux quelconques de ces vecteurs sont égaux, il vaut 0.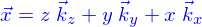 ,
,  et
et 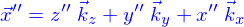 se calcule comme le déterminant
se calcule comme le déterminant
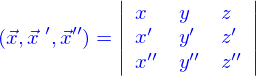
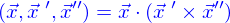
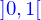 par une application
par une application
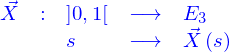
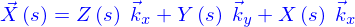
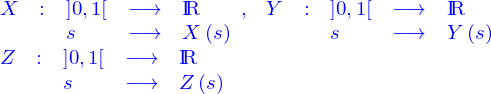

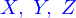 . Sans elle, la ligne comporte plusieurs morceaux, elle est dite non
. Sans elle, la ligne comporte plusieurs morceaux, elle est dite non 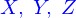 . Sans elle, la ligne n'admet pas de tangente.
. Sans elle, la ligne n'admet pas de tangente.  ne s'annulent pas simultanément. Sinon il y a des
ne s'annulent pas simultanément. Sinon il y a des  . Sinon il y a des points doubles ou pire encore.
. Sinon il y a des points doubles ou pire encore.
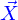 . C'est la fonction
. C'est la fonction
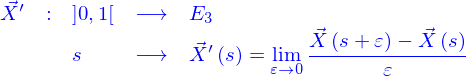
 et lorsqu'elles existent pour tout les
et lorsqu'elles existent pour tout les  de l'intervalle
de l'intervalle 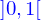 on dit que ces fonctions sont dérivables dans cet intervalle.
on dit que ces fonctions sont dérivables dans cet intervalle.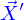 existe, on peut associer à chacun des points
existe, on peut associer à chacun des points 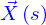 une droite qui est une nouvelle ligne définie paramétriquement comme indiqué sur la figure. Cette droite est appelée la droite tangente à la ligne en
une droite qui est une nouvelle ligne définie paramétriquement comme indiqué sur la figure. Cette droite est appelée la droite tangente à la ligne en 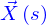 .
.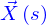 ; c'est à dire que pour les positions suffisamment proches de
; c'est à dire que pour les positions suffisamment proches de  la ligne ne diffère pas sensiblement de sa droite tangente en cette position.
la ligne ne diffère pas sensiblement de sa droite tangente en cette position.
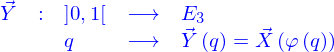
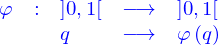

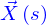 de ne pas le faire dépendre de
de ne pas le faire dépendre de  mais de
mais de 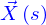 , soit d'introduire
, soit d'introduire
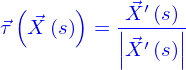
 , on peut écrire (par la
, on peut écrire (par la 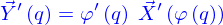
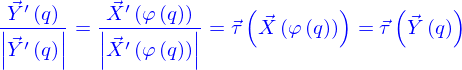
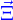 un point de la ligne (qui peut être obtenu par une paramétrisation de celle-ci comme
un point de la ligne (qui peut être obtenu par une paramétrisation de celle-ci comme 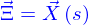 ), on peut donc lui associer le vecteur tangent à la ligne qui est
), on peut donc lui associer le vecteur tangent à la ligne qui est 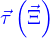 (ce vecteur pouvant être obtenu par la paramétrisation comme
(ce vecteur pouvant être obtenu par la paramétrisation comme 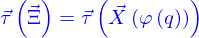 ).
).
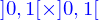 par une application
par une application
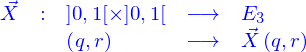
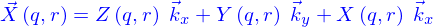

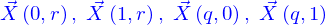 : ces lignes sont les lignes extrémités de la nappe, on dit que l'ensemble qu'elles forment est le bord de la nappe. Comme on n'a pas inclus les valeur 0 et 1 dans le domaine de définition de l'application
: ces lignes sont les lignes extrémités de la nappe, on dit que l'ensemble qu'elles forment est le bord de la nappe. Comme on n'a pas inclus les valeur 0 et 1 dans le domaine de définition de l'application 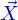 , ces lignes sont obtenues par un passage aux limites (comme pour les lignes).
, ces lignes sont obtenues par un passage aux limites (comme pour les lignes).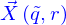 : cette ligne est la ligne décrite par la variable
: cette ligne est la ligne décrite par la variable  lorsque la variable
lorsque la variable
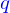 est fixée à la valeur constante
est fixée à la valeur constante  .
.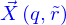 : idem en changeant les
: idem en changeant les 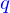 en
en  et vice-versa.
et vice-versa.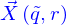 obtenues lorsqu'on fait varier
obtenues lorsqu'on fait varier 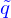 entre 0 et 1 forme ce qu'on appelle une famille de courbes. Mais l'ensemble contient aussi les points de la nappe.
entre 0 et 1 forme ce qu'on appelle une famille de courbes. Mais l'ensemble contient aussi les points de la nappe.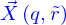 .
.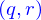 : soit on introduit une application
: soit on introduit une application 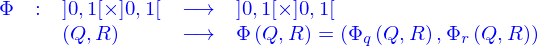
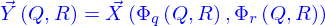
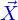 , un point de la nappe est repéré par une valeur de
, un point de la nappe est repéré par une valeur de 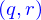 . Ce point est l'intersection des deux lignes :
. Ce point est l'intersection des deux lignes :  et
et  .
.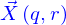 : pour la première, par rapport à
: pour la première, par rapport à  ; pour la seconde, par rapport à
; pour la seconde, par rapport à  . On les note
. On les note
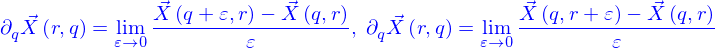
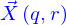 . Il est donc nécessaire que
. Il est donc nécessaire que
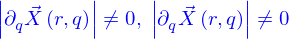
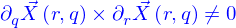
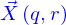 , c'est
, c'est

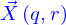 sur la nappe et non pas des
sur la nappe et non pas des  parce qu'il ne dépend pas de la paramétrisation utilisée. On peut faire un calcul (analogue à celui qui a été fait pour montrer que le vecteur tangent à une ligne ne dépend pas non plus de la paramétrisation de la ligne) pour le montrer, c'est laissé en exercice.
parce qu'il ne dépend pas de la paramétrisation utilisée. On peut faire un calcul (analogue à celui qui a été fait pour montrer que le vecteur tangent à une ligne ne dépend pas non plus de la paramétrisation de la ligne) pour le montrer, c'est laissé en exercice.
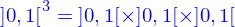 par une application
par une application
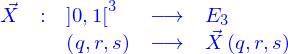
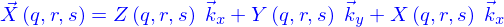
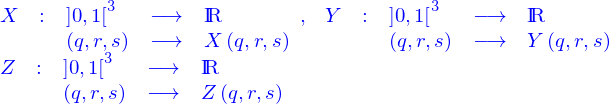
 et le paramètre supplémentaire qui indexe les nappes dans la famille est
et le paramètre supplémentaire qui indexe les nappes dans la famille est 
 ou encore
ou encore 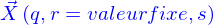
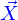 soit la paramétrisation d'un domaine est déjà que les éléments de ces familles soient vraiment des nappes. Et il faut aussi ajouter que le paramètre d'indexation des nappes dans une famille conduit bien à former des nappes différentes lorsqu'il varie.
soit la paramétrisation d'un domaine est déjà que les éléments de ces familles soient vraiment des nappes. Et il faut aussi ajouter que le paramètre d'indexation des nappes dans une famille conduit bien à former des nappes différentes lorsqu'il varie. 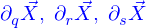 soit non nul, soit
soit non nul, soit
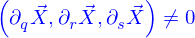
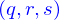 .
.

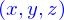 , on l'appelle
, on l'appelle

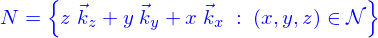
 et/ou l'expression qu'on lui donne, l'ensemble
et/ou l'expression qu'on lui donne, l'ensemble  peut être
peut être
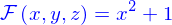
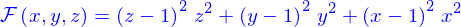
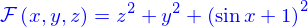
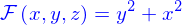
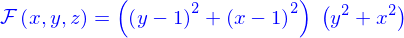
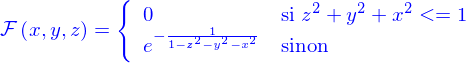
 soit une nappe et rien d'autre.
soit une nappe et rien d'autre.
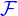 par rapport aux coordonnées
par rapport aux coordonnées  ne s'annulent pas toutes simultanément lorsque
ne s'annulent pas toutes simultanément lorsque 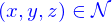
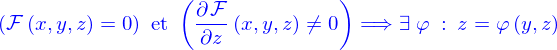
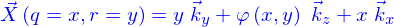
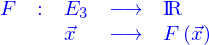
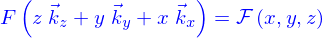
 le vecteur dépendant de la position (on dira le champ de vecteurs plus loin) défini par
le vecteur dépendant de la position (on dira le champ de vecteurs plus loin) défini par
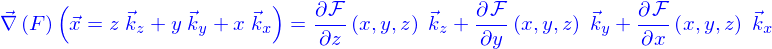

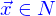 . Avec la définition implicite, ce vecteur normal d'exprime comme
. Avec la définition implicite, ce vecteur normal d'exprime comme

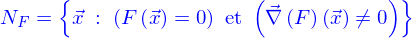
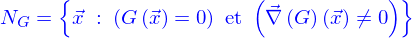

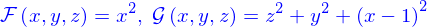
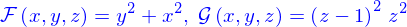
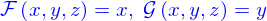
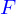 et
et  ne soit pas nul aux points d'intersection. Ce produit vectoriel permet de trouver le vecteur tangent aux points de la ligne, définis par
ne soit pas nul aux points d'intersection. Ce produit vectoriel permet de trouver le vecteur tangent aux points de la ligne, définis par
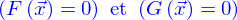
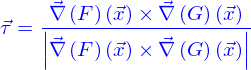 On aurait également pu choisir l'opposé de ce vecteur
On aurait également pu choisir l'opposé de ce vecteur
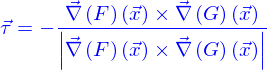 comme vecteur tangent. La définition de la ligne comme intersection de deux nappes ne dit rien de l'orientation de cette ligne, c'est laissé libre.
comme vecteur tangent. La définition de la ligne comme intersection de deux nappes ne dit rien de l'orientation de cette ligne, c'est laissé libre.
 est dit borné si
est dit borné si

 borné défini paramétriquement à partir de l'application (différentiable)
borné défini paramétriquement à partir de l'application (différentiable)
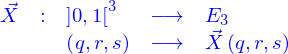
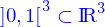 par l'application
par l'application  , soit
, soit
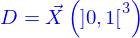
 doit (je n'en suis pas sûr mais ça semble raisonnable) admettre une limite lorsque les
doit (je n'en suis pas sûr mais ça semble raisonnable) admettre une limite lorsque les  atteignent 0 ou 1.
atteignent 0 ou 1. est l'ensemble
est l'ensemble

 des 6 facettes du cube
des 6 facettes du cube  .
.
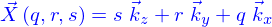
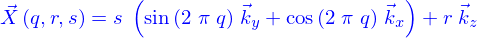
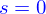 est le segment
est le segment 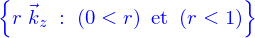 . De plus les facettes
. De plus les facettes  et
et  coïncident, c'est le rectangle
coïncident, c'est le rectangle 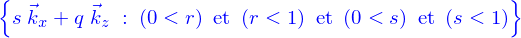 .
.
 contient bien les facettes du cube mais pas ses arêtes. On peut toujours essayer de lui ajouter ces 12 arêtes, mais alors quelle serait le vecteur normal sur elles ?
contient bien les facettes du cube mais pas ses arêtes. On peut toujours essayer de lui ajouter ces 12 arêtes, mais alors quelle serait le vecteur normal sur elles ?
 ne permet pas d'identifier simplement leurs bords.
ne permet pas d'identifier simplement leurs bords. 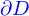 de ce domaine est l'ensemble des points tels que, si petite soit la boule qu'on forme avec ces points aux centres, celle-ci contiendra à la fois des points du domaine et des points qui ne lui appartiennent pas.
de ce domaine est l'ensemble des points tels que, si petite soit la boule qu'on forme avec ces points aux centres, celle-ci contiendra à la fois des points du domaine et des points qui ne lui appartiennent pas.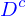 du domaine est l'ensemble des points qui n'appartiennent pas au domaine telsqu'on puisse toujours trouver une boule suffisamment petite pour que tous les points de la boule soient extérieurs au domaine.
du domaine est l'ensemble des points qui n'appartiennent pas au domaine telsqu'on puisse toujours trouver une boule suffisamment petite pour que tous les points de la boule soient extérieurs au domaine.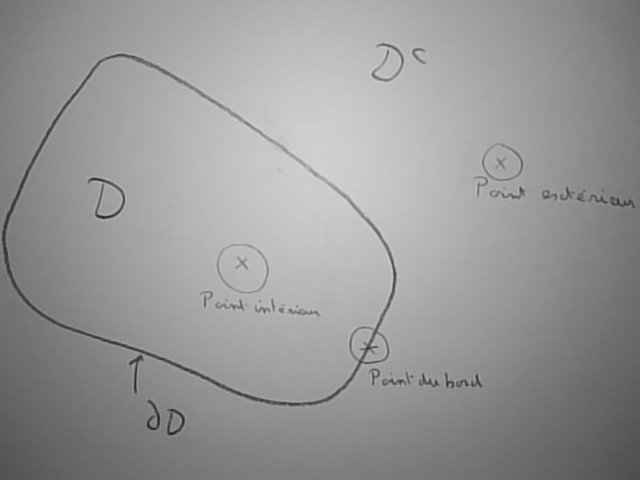

 ) puisse être déformée par petites étapes (on dit continûment) jusqu'à pouvoir être réduite à un seul point sans jamais que les points qui la composent cessent d'être des points du domaine. Mais cela suppose de définir ce qu'on a appellé une déformation, ce qui nous emmènerait trop loin.
) puisse être déformée par petites étapes (on dit continûment) jusqu'à pouvoir être réduite à un seul point sans jamais que les points qui la composent cessent d'être des points du domaine. Mais cela suppose de définir ce qu'on a appellé une déformation, ce qui nous emmènerait trop loin.




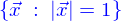


 est
est
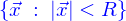
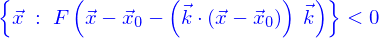
 est un point de l'espace et
est un point de l'espace et 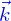 un vecteur tel que
un vecteur tel que 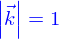 quelconque.
quelconque.
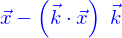 est la projection de
est la projection de 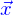 dans le plan passant par l'origine et normal à
dans le plan passant par l'origine et normal à 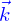 ; et on peut dire la même chose en remplaçant
; et on peut dire la même chose en remplaçant 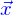 par
par  à ceci près que le vecteur projeté est
à ceci près que le vecteur projeté est 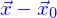 et que le plan passe par
et que le plan passe par 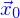 .
.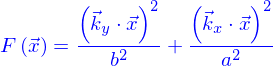 et
et 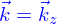
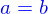 ).
).
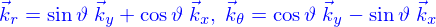
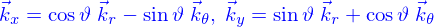
 peut alors s'écrire
peut alors s'écrire
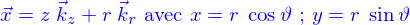
 qui s'appellent les coordonnées cylindriques de
qui s'appellent les coordonnées cylindriques de 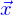 .
.
 . Cet axe est exclu de l'ensemble d'arrivée parce que la valeur
. Cet axe est exclu de l'ensemble d'arrivée parce que la valeur  est exclue de l'ensemble de départ. L'application est continue et différentiable (indéfiniment) et bijective sur les ensemble de départ et d'arrivée spécifiés. Son inverse (également différentiable) peut être construit avec
est exclue de l'ensemble de départ. L'application est continue et différentiable (indéfiniment) et bijective sur les ensemble de départ et d'arrivée spécifiés. Son inverse (également différentiable) peut être construit avec
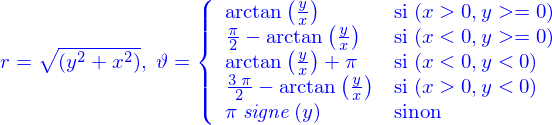
 correspond à
correspond à
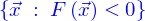
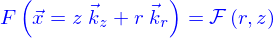

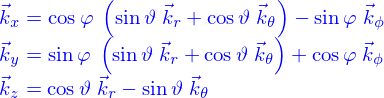
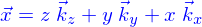 peut alors s'écrire
peut alors s'écrire
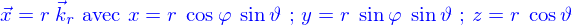
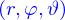 qui s'appellent les coordonnées sphériques de
qui s'appellent les coordonnées sphériques de  .
.
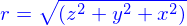 ; l'angle
; l'angle  se trouve avec la même formule que pour le
se trouve avec la même formule que pour le 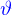 des coordonnées cylindriques ; et l'angle
des coordonnées cylindriques ; et l'angle 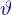 par une formule analogue quoique plus simple puisque
par une formule analogue quoique plus simple puisque 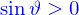 .
.

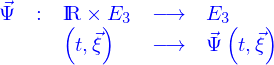
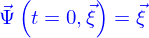
 se retrouve au temps
se retrouve au temps  en
en  .
.
 est supposée bijective et différentiable (au moins deux fois) et d'inverse différentiable et cela à la fois par rapport à la variable de temps
est supposée bijective et différentiable (au moins deux fois) et d'inverse différentiable et cela à la fois par rapport à la variable de temps  et d'espace
et d'espace 
 est
est
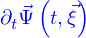
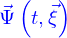 et cela pour toutes les positions possibles. Cela revient à introduire l'application
et cela pour toutes les positions possibles. Cela revient à introduire l'application
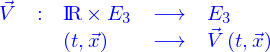
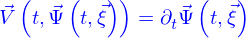
 mais par le champ de vitesses eulérien
mais par le champ de vitesses eulérien  et alors l'application
et alors l'application  est à trouver comme solution de l'ensemble continu d'équations différentielles ordinaires
est à trouver comme solution de l'ensemble continu d'équations différentielles ordinaires

 est alors appelée le flot du champ de vecteurs
est alors appelée le flot du champ de vecteurs  .
.
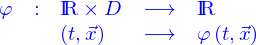
 est un domaine. La dépendance en
est un domaine. La dépendance en  est à comprendre comme celle de la fonction
est à comprendre comme celle de la fonction 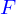 vis-à-vis de la fonction
vis-à-vis de la fonction 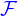 utilisée pour la définition implicite des nappes, soit
utilisée pour la définition implicite des nappes, soit
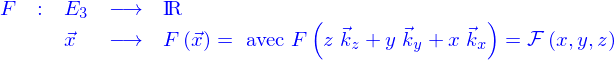
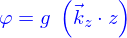 à partir duquel le champ de pesanteur est
à partir duquel le champ de pesanteur est 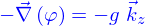 ;
; qui représente un certain volume d'eau.
qui représente un certain volume d'eau. mais on va plutôt utiliser
mais on va plutôt utiliser  , soit
, soit
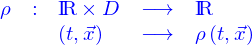
 la dénotation d'être une densité de quantité, suppose qu'on introduise déjà la quantité dont elle est la densité. Cette quantité peut être n'importe quelle
la dénotation d'être une densité de quantité, suppose qu'on introduise déjà la quantité dont elle est la densité. Cette quantité peut être n'importe quelle 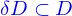 défini paramétriquement par
défini paramétriquement par

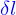 est très petit, la valeur de
est très petit, la valeur de  (supposée continue) ne varie pas beaucoup dans le cube, et donc la quantité que ce cube contient est
(supposée continue) ne varie pas beaucoup dans le cube, et donc la quantité que ce cube contient est
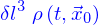
 peut être pavé par de tels petits cubes, on peut obtenir la quantité contenue par
peut être pavé par de tels petits cubes, on peut obtenir la quantité contenue par  en sommant toutes les contributions des petits cubes formés en faisant varier
en sommant toutes les contributions des petits cubes formés en faisant varier 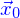 .
. est défini paramétriquement comme l'image de l'intervalle
est défini paramétriquement comme l'image de l'intervalle 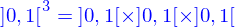 par une application
par une application
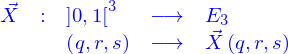
 , par exemple
, par exemple
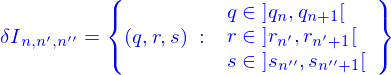
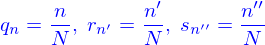
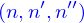 sont des entiers allant de
sont des entiers allant de  à
à  et où
et où  est un nombre entier qui peut être choisi aussi grand qu'on veut pour que les cubes
est un nombre entier qui peut être choisi aussi grand qu'on veut pour que les cubes  soient aussi petits qu'on veut.
soient aussi petits qu'on veut.
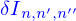 par l'application
par l'application 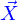 n'est pas un cube. Mais si
n'est pas un cube. Mais si  est très grand,
est très grand, 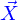 varie suffisamment peu pour qu'on puisse approximer l'image des arêtes du cube
varie suffisamment peu pour qu'on puisse approximer l'image des arêtes du cube 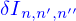 par des segments droits. On obtient donc que cette image est un parallépipède de base les
par des segments droits. On obtient donc que cette image est un parallépipède de base les
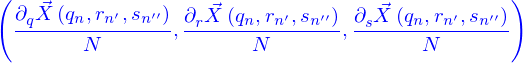
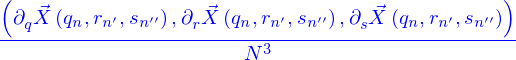
 ne varie pas sensiblement sur toute son étendue, et donc la contribution de l'image par
ne varie pas sensiblement sur toute son étendue, et donc la contribution de l'image par  du petit cube
du petit cube  à la quantité cherchée est
à la quantité cherchée est

 , il suffit de sommer sur tout les cubes
, il suffit de sommer sur tout les cubes 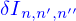 pour obtenir
pour obtenir
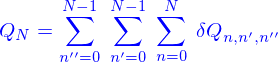
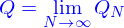

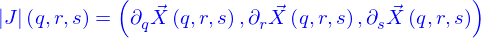
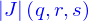 est appelé le
est appelé le  .
.
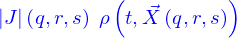 on peut calculer la quantité
on peut calculer la quantité  .
.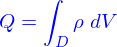
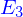 un champ de vitesses eulérien
un champ de vitesses eulérien

 une quantité qui est répartie avec la densité
une quantité qui est répartie avec la densité 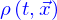 .
.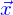 à l'instant
à l'instant  , elle se retrouvera en
, elle se retrouvera en 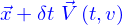 à l'instant
à l'instant 
 décrite paramétriquement par
décrite paramétriquement par 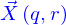 entre les instants
entre les instants  et
et  , étant petit
, étant petit
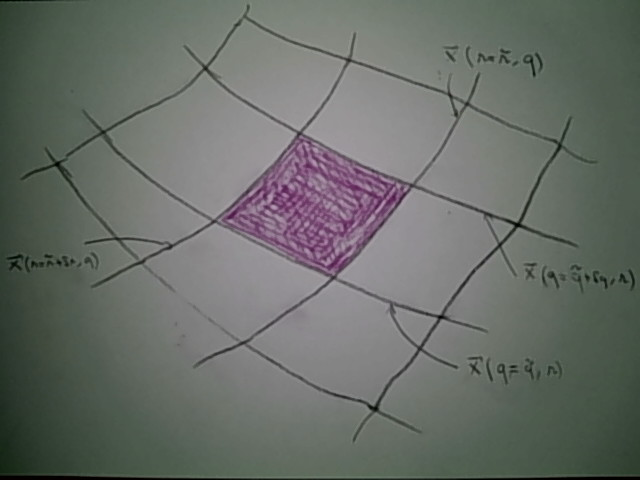
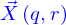 pour
pour 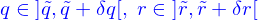 ,
, 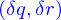 étant petits.
étant petits.
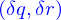 sont effectivement petits l'approximation pour laquelle il l'est est acceptable. On la fait. Cela permet déjà d'affirmer que sa contribution à la surface de la nappe est
sont effectivement petits l'approximation pour laquelle il l'est est acceptable. On la fait. Cela permet déjà d'affirmer que sa contribution à la surface de la nappe est

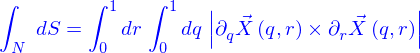
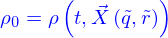 . Cela rend possible le calcul du nombre de particules qui traversent le parallélogramme.
. Cela rend possible le calcul du nombre de particules qui traversent le parallélogramme.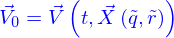 , il s'exprime à partir du vecteur
, il s'exprime à partir du vecteur 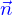 normal à ce parallélogramme comme
normal à ce parallélogramme comme

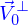 est la projection du vecteur
est la projection du vecteur 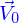 sur le plan du parallélogramme.
sur le plan du parallélogramme.
 sont celle qui sont situées dans le volume situé en dessous (par rapport à la direction du vecteur
sont celle qui sont situées dans le volume situé en dessous (par rapport à la direction du vecteur 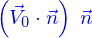 ) de celui-ci et de profondeur
) de celui-ci et de profondeur 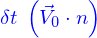

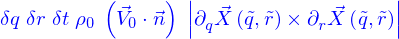
 , mais c'est dans le sens du plan tangent au parallélograme et donc ça ne contribue pas au nombre de particules qui le traversent.)
, mais c'est dans le sens du plan tangent au parallélograme et donc ça ne contribue pas au nombre de particules qui le traversent.)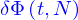 de particules qui traversent la nappe à l'instant
de particules qui traversent la nappe à l'instant  pendant le laps de temps
pendant le laps de temps  . C'est
. C'est
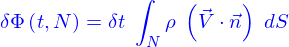
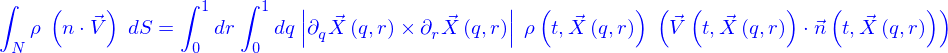
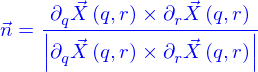
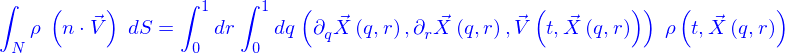
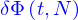 , porte à considérer la densité de flux advectif de particules
, porte à considérer la densité de flux advectif de particules

 et par
et par 
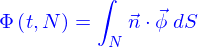
 par seconde, ou encore le débit de particules. À partir de ce flux advectif on obtient le nombre de particules qui traversent
par seconde, ou encore le débit de particules. À partir de ce flux advectif on obtient le nombre de particules qui traversent  de
de  à
à  par
par
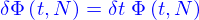
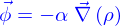
 est appelé la diffusivité (en
est appelé la diffusivité (en  ; c'est une constante positive caractéristique du type de densité à laquelle on associe un mécanisme de conduction.
; c'est une constante positive caractéristique du type de densité à laquelle on associe un mécanisme de conduction. est le gradient de
est le gradient de  . On a déjà vu ce qu'était un gradient lorsqu'on a représenté implicitement une nappe. Ce gradient a exactement la même expression. Soit, si (on utilise le même symbole
. On a déjà vu ce qu'était un gradient lorsqu'on a représenté implicitement une nappe. Ce gradient a exactement la même expression. Soit, si (on utilise le même symbole  à gauche et à droite pour éviter d'alourdir)
à gauche et à droite pour éviter d'alourdir)
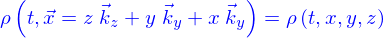
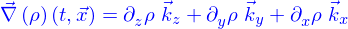
 mais ceux-ci sont
mais ceux-ci sont  .
.
 , que la densité est une densité de particules, le nombre de particules qui traversent la nappe par unité de temps (son flux ou encore débit) est
, que la densité est une densité de particules, le nombre de particules qui traversent la nappe par unité de temps (son flux ou encore débit) est
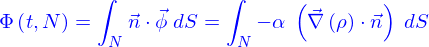
 dont la densité de flux est
dont la densité de flux est  , qu'il soit advectif ou diffusif. Cette densité s'écrit en composantes
, qu'il soit advectif ou diffusif. Cette densité s'écrit en composantes
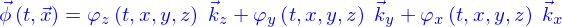
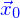 et de longueur d'arêtes
et de longueur d'arêtes 

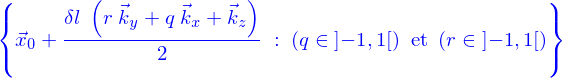

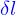 de
de  est
est
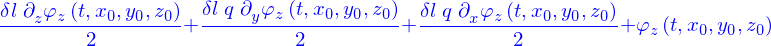


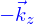 et non plus
et non plus 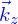 comme pour la première.
comme pour la première.
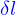 de
de  est
est



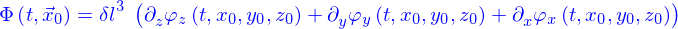
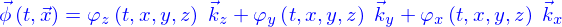
 de bord
de bord  et pour tout champ de vecteurs
et pour tout champ de vecteurs 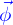 on a
on a
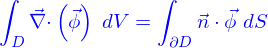
 est petit
est petit

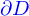 est la réunion des 6 facettes précédente, d'où
est la réunion des 6 facettes précédente, d'où
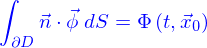
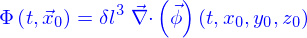
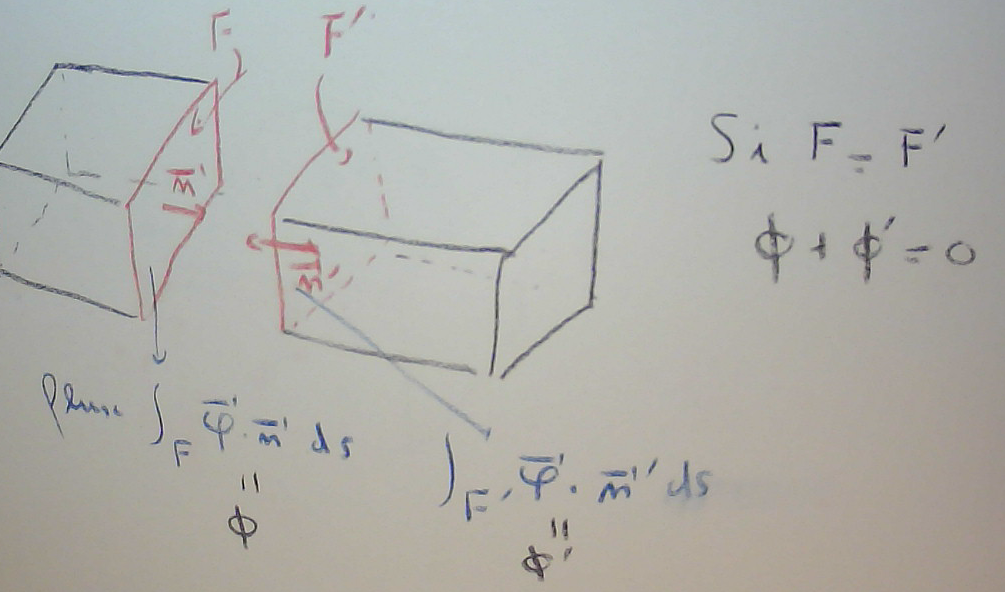
 qui est formé de la justaposition d'un nombre quelconque de petits cubes. En 2 dimensions
qui est formé de la justaposition d'un nombre quelconque de petits cubes. En 2 dimensions
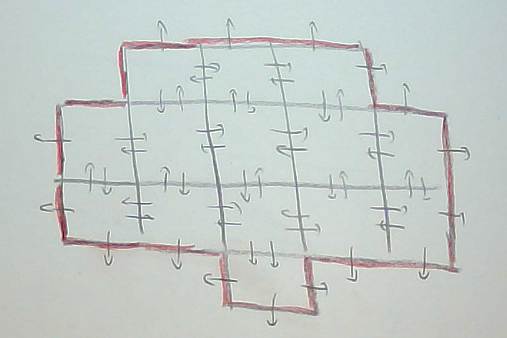
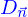 des petits cubes (où
des petits cubes (où  est le numéro du cube). On voit alors qu'en sommant sur
est le numéro du cube). On voit alors qu'en sommant sur  les relations
les relations
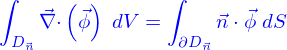
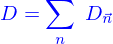
 est composé des facettes en rouge du dessin.
est composé des facettes en rouge du dessin.
 devient lisse (son bord peut être assimilé à une nappe lisse, c'est à dire paramétrable par une donction différentiable) et on obtient le résultat
devient lisse (son bord peut être assimilé à une nappe lisse, c'est à dire paramétrable par une donction différentiable) et on obtient le résultat
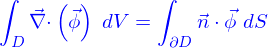
 avec la densité
avec la densité  était
était

 de cette quantité à travers le bord
de cette quantité à travers le bord  de ce domaine est
de ce domaine est
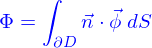
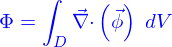
 par unité de temps. Mais ce nombre est aussi
par unité de temps. Mais ce nombre est aussi
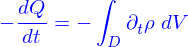
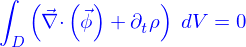
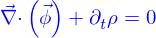
 alors
alors 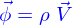 et
et
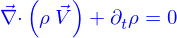
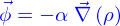 où
où  est la diffusivité et
est la diffusivité et
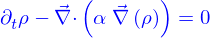
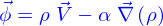 on obtient
on obtient

 et ses dérivées partielles. Par exemple
et ses dérivées partielles. Par exemple
 est un temps et
est un temps et  des distances). On ne s'occupera pas de tels formes.
des distances). On ne s'occupera pas de tels formes.
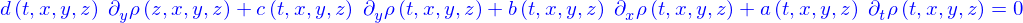
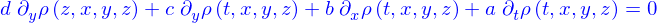
 pour que les expressions soient plus lisibles.
pour que les expressions soient plus lisibles.
 ; il peut dépendre de
; il peut dépendre de  .
.
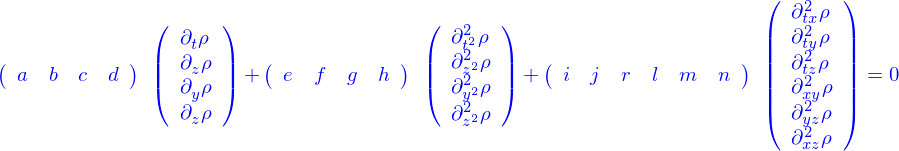
 l'égalité se fait avec ce
l'égalité se fait avec ce  plutôt que 0.
plutôt que 0.
 . Il est défini sur un domaine
. Il est défini sur un domaine  et cherché comme solution de
et cherché comme solution de
 le champ de scalaire défini par
le champ de scalaire défini par


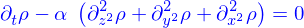

 et les points du bord
et les points du bord  de ce domaine n'appartiennent pas au domaine. Il faut donc ajouter à l'équation de diffusion des conditions pour espérer obtenir une solution qui ne comporte pas de contantes indéterminées.
de ce domaine n'appartiennent pas au domaine. Il faut donc ajouter à l'équation de diffusion des conditions pour espérer obtenir une solution qui ne comporte pas de contantes indéterminées.  sont appelées des conditions aux limites.
sont appelées des conditions aux limites. 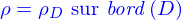
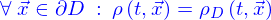
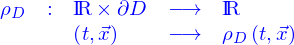
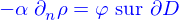
 est une notation pour
est une notation pour

 étant la normale de
étant la normale de  dirigée vers l'extérieur de
dirigée vers l'extérieur de  ; où la signification de « sur » est, comme pour la condition de Dirichlet,
; où la signification de « sur » est, comme pour la condition de Dirichlet,
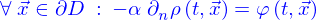
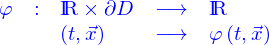
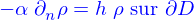
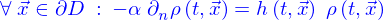
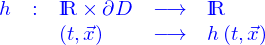
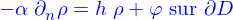
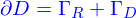
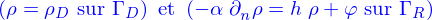
 est nécessaire pour espérer obtenir une solution dépouvue de constantes indéterminées à un problème de diffusion dans un domaine
est nécessaire pour espérer obtenir une solution dépouvue de constantes indéterminées à un problème de diffusion dans un domaine  pourvu de conditions aux limites sur son bord
pourvu de conditions aux limites sur son bord  . C'est la condition initiale
. C'est la condition initiale
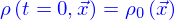

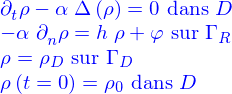
 soient à valeurs strictement positives, ce système d'équation admet une solution unique.
soient à valeurs strictement positives, ce système d'équation admet une solution unique.
 ne dépendent pas du tempsm cette solution finit par ne plus dépendre du temps, soit
ne dépendent pas du tempsm cette solution finit par ne plus dépendre du temps, soit
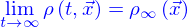
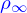 est solution de
est solution de

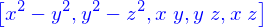

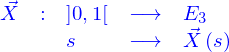
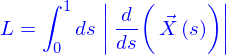
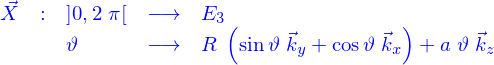
 spires d'hélice de rayon et pas
spires d'hélice de rayon et pas  , le rayon diminue et le pas s'allonge sans que la longueur de l'hélice par laquelle on représente le ressort ne change. On allonge donc le ressort de
, le rayon diminue et le pas s'allonge sans que la longueur de l'hélice par laquelle on représente le ressort ne change. On allonge donc le ressort de 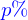 de sa longueur initiale, quelle est la variation de rayon ?
de sa longueur initiale, quelle est la variation de rayon ? 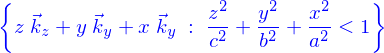
 )
)
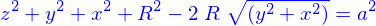
 , rayon
, rayon  ) qui forme un domaine
) qui forme un domaine 
 , le bord de
, le bord de  et donner son champ de normales (orienté vers l'extérieur du domaine)
et donner son champ de normales (orienté vers l'extérieur du domaine) 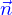
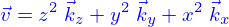 , calculer
, calculer 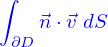

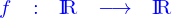 , dérivable deux fois. Montrer que
, dérivable deux fois. Montrer que 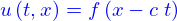 est solution de
est solution de 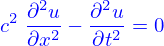
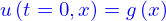
 est une fonction quelconque.
est une fonction quelconque.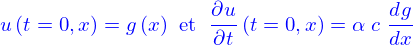
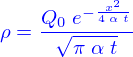 est solution de
est solution de 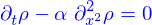
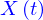 défini par
défini par 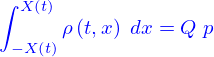 où
où 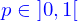
 qu’on remplit d’eau pure jusqu’`a une hauteur
qu’on remplit d’eau pure jusqu’`a une hauteur 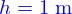 comptée à partir de l’interface sel/eau.
comptée à partir de l’interface sel/eau. 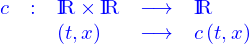
 où
où  est la coordonnée dans la direction de l'axe de l'éprouvette (
est la coordonnée dans la direction de l'axe de l'éprouvette ( 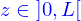 et
et 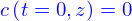 .
. 
 .
. 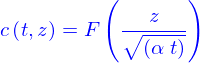 où
où  est une fonction à déterminer.
est une fonction à déterminer.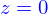 comme la quantité
comme la quantité 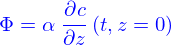 (c'est la quantité de sel qui entre dans l'eau par unité de surface de la section de l'éprouvette. Calculer
(c'est la quantité de sel qui entre dans l'eau par unité de surface de la section de l'éprouvette. Calculer 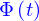 . Que se passe-t'il en
. Que se passe-t'il en 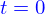 ?
? 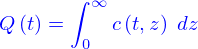 . Calculer
. Calculer 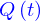
 et
et  ?
?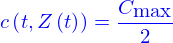 . Suivant quelle loi
. Suivant quelle loi  dépend-t'il du temps ?
dépend-t'il du temps ?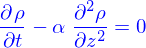
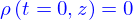
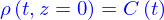
 est un fonction donnée.
est un fonction donnée.
 (notée
(notée  ) est solution.
) est solution. en fonction de
en fonction de  (la transformée de Laplace de
(la transformée de Laplace de  )
)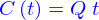 , donner l'expression de
, donner l'expression de 

 fonction quelconque, trouver une relation entre
fonction quelconque, trouver une relation entre  ,
, 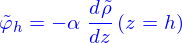 et
et 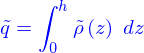
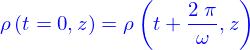
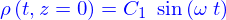
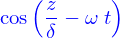 dès lors que
dès lors que  prend une valeur à préciser.
prend une valeur à préciser.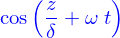 ,
, 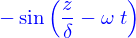 et
et 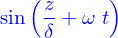 ?
?