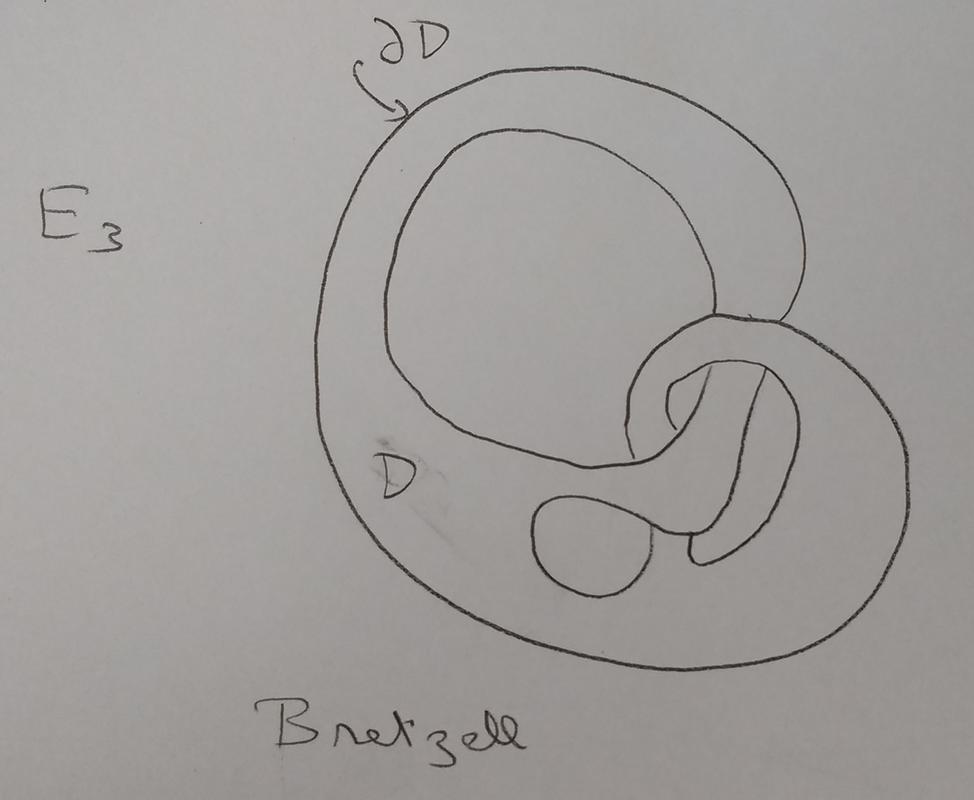
L'approche discrète d'un problème physique consiste à représenter un phénomène par un nombre fini de variables (de phase : i.e. les variables de configuration et les variables de vitesse) et à établir des relations (différentielles ou non) entre ces variables. Ces relations forment un système d'Équations Différentielles Ordinaires. (EDP)
C'est ce qu'on fait en mécanique des solides indéformables et en circuit électrique.
Mais cette approche échoue dans certains cas. Par exemple quelle sont les forces de réaction que le sol exerce sur les pattes de la chaise supposée indéformable lorsqu'on pose un objet lourd (le penseur, les penseurs sont généralement lourds. On le suppose de plus indéformable, ce qui est également une caractéristique courante du genre) en une position quelconque de l'assise ?

Il y a a priori au moins 4 composantes verticales de forces de réaction et l'équilibre du solide indéformable composé de la chaise et du penseur (vissé à la chaise, c'est assez fréquent chez les penseurs) fournit 3 équations. Il en manque donc une !
On peut résoudre ce genre de difficultés (l'hyperstaticité) en supposant que les pattes sont des ressorts. Cela complique un peu le problème mais on trouve alors une solution.
Mais celle-ci n'est pas tout à faite satisfaisante. Pourquoi ne pas conférer plutôt à l'assise la nature d'un ressort ? Et comment d'aillers pourrait procéder pour le faire ?
Dans un cas de ce genre, on renonce à supposer que la chaise est un solide indéformable et on accepte donc qu'elle se déforme (le penseur reste lui indéformable). Mais alors chacun des points de la chaise se déplace. Et ces déplacements forment un ensemble infini de variables de configuration.
Ce n'est plus une approche discrète mais une approche continue. Continue parce qu'on va supposer que les déplacements de deux points très proches de la chaise ont des déplacements également très proches l'un de l'autre.
Les équations permettant de trouver effectivement ces déplacements seront alors formulés comme la recherche d'une fonction
![block([],addv(u,x),DefFonc(u,D,E3,x,u(x)))](EDOetEDP/eq5.png)
 est le domaine de l'espace
est le domaine de l'espace 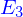
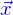 est le point courant dans
est le point courant dans 
Cette fonction 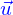 traduit le déplacement de
traduit le déplacement de  ; c'est à dire que le point
; c'est à dire que le point  de la chaise avant qu'on lui place le penseur dessus se retrouvera en
de la chaise avant qu'on lui place le penseur dessus se retrouvera en
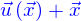 après qu'elle soit ainsi chargée par lui.
après qu'elle soit ainsi chargée par lui.
Pour trouver les équations permettant le calcul de 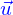 , il faudra écrire l'équilibre de chacun des domaines infinitésimaux autour des différents points
, il faudra écrire l'équilibre de chacun des domaines infinitésimaux autour des différents points 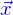 de
de  et ces équilibres fourniront suffisamment d'équations locales pour que
et ces équilibres fourniront suffisamment d'équations locales pour que 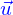 puisse être déterminé.
puisse être déterminé.
La façon de procéder est expliquée dans la leçon sur l'élasticité. Elle conduit à un système d'Équations aux Dérivées Partielles (EDP) muni de conditions aux limites. C'est un premier exemple d'équation macroscopique de la physique classique.
Mais, pour en revenir au problème de départ, on ne demande pas qu'une solution 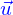 , on demande surtout qu'elle permette de calculer correctement les forces de réactions sur les pattes de la chaise.
, on demande surtout qu'elle permette de calculer correctement les forces de réactions sur les pattes de la chaise.
Il ne suffit donc pas de savoir résoudre les équations, il faut encore comprendre suffisamment bien leur structure pour qu'elles apportent des réponses à des problèmes relativement simples à poser (quelles sont les forces de réaction ?) mais dont la réponse est nettement moins simple à obtenir.
Dans l'idéal, le cours sur les EDPs devrait avoir eu lieu. Et donc tout le monde saurait ce qu'est (pour les mathématiciens) un ouvert connexe  de l'espace
de l'espace 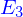 ; une EDP de type elliptique portant sur une variable vectorielle et munie des conditions aux limites mixtes (Dirichlet et Neuman) ; les espaces fonctionnels ad hoc pour que ces problèmes puissent être aisément résolus par éléments finis et tutti quanti.
; une EDP de type elliptique portant sur une variable vectorielle et munie des conditions aux limites mixtes (Dirichlet et Neuman) ; les espaces fonctionnels ad hoc pour que ces problèmes puissent être aisément résolus par éléments finis et tutti quanti.
Mais bien évidemment on est, hic et nunc, plutôt plongé dans le spleen (comme le penseur). Aussi doit-on adopter une attitude raisonnable et pragmatique.
Ceci étant dit, les premières notions dont on doit pouvoir disposer sont celles qui permettent la description géométrique d'objet. Et d'abord celle du domaine  de l'espace
de l'espace 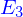
.
La chaise est un peu compliquée (sa forme et le fait qu'elle soit composée de plusieurs matériaux plus ou moins bien reliés entre eux) prenons un objet plus simple : le domaine liquide d'un verre d'eau.

En première approximation, c'est un tronçon de cylindre à section circulaire. On choisit l'origine à partir de laquelle partent les vecteurs positions au milieu d'une des bases ; une base orthonormée de vecteurs 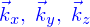 de manière que
de manière que 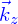 soit le vecteur directeur de l'axe de symétrie du cylindre (l'axe autour duquel on peut faire une rotation qui laisse globalement invariante le cylindre).
soit le vecteur directeur de l'axe de symétrie du cylindre (l'axe autour duquel on peut faire une rotation qui laisse globalement invariante le cylindre).
Ainsi le domaine  de hauteur h et de rayon R est (voir pour les notations)
de hauteur h et de rayon R est (voir pour les notations)
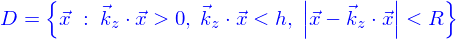
Et le bord du domaine est
![block([],Indicie([0,1,](EDOetEDP/eq28.png)
![block([],Indicie([0,1,](EDOetEDP/eq25.png) ,
,
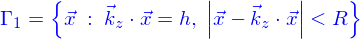 et
et
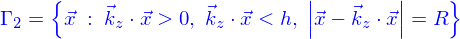
Les coordonnées cartésiennes seraient peu adaptées, aussi, utilise-t'on les coordonnées cylindriques (voir encore) qui permettent d'écrire
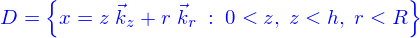
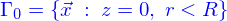 ,
,
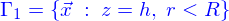 et
et
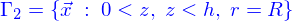
Supposons maintenant que le verre d'eau soit placé sur un plateau tournant de manière que l'axe de symétrie du domaine  coïncide avec l'axe de rotation du plateau. Du fait de la force centrifuge le domaine
coïncide avec l'axe de rotation du plateau. Du fait de la force centrifuge le domaine  sera déformé mais il restera invariant en rotation : on appelle ce genre de symétrie la symétrie axisymétrique.
sera déformé mais il restera invariant en rotation : on appelle ce genre de symétrie la symétrie axisymétrique.
Il y aura donc une certaine fonction
![DefFonc(Z,[0,R],Reel,r,Z(r))](EDOetEDP/eq33.png)
 comme
comme
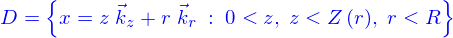
Par contre il est intéressant de noter qu'au bout d'un certain temps l'eau tourne comme si elle était un solide. La vitesse d'un point de  est alors
est alors
![block([],addv(v),v=Omega*r*kt)](EDOetEDP/eq35.png)
 est la vitesse de rotation du plateau tournant.
est la vitesse de rotation du plateau tournant.
La description précédente est valable tant que la force centrifuge n'est pas suffisante pour éjecter toute l'eau ou presque sur le bord latéral du verre.
Examinons encore une situation plus complexe, où le verre n'est pas disposé au centre du plateau tournant. La géométrie de  cessera d'être axisymétrique mais par contre la vitesse de l'eau sera celle d'un solide.
cessera d'être axisymétrique mais par contre la vitesse de l'eau sera celle d'un solide.
Cette première leçon introductive à l'enseignement d'Équations Macroscopiques de la Physique Classique n'introduit aucune des notions qui seront amenée et développées dans les leçons suivantes.
Par contre elle tente de donner une idée de l'esprit dans lequel devront être abordés ces leçons. On s'attachera à énumérer une série de problématiques générales (comment coulent les fluides, comment se déforment les solides, comment diffusent les particules ...) et pour chacune d'elles on introduira un caneva descriptif à base d'équations qui est exactement ce qu'on appelle une modélisation.
La question de la description de géométrie sera récurente. Et cette leçon a aussi pour objectif de vous inciter à réfléchir en amont sérieusement à cela.
Pour ne pas tourner à vide, trois petits thèmes de réflexion (en rouge) sont fournis qui devraient vous faire passer agréablement le temps en autonomie.
Et au cas où ceux-ci serait trop simple, voici quelque-chose de plus compliqué