Planche 1 : Voici le second cours de ces deux cours magistraux dans le cadre du cours de CAO.

Il porte sur l'induction électromagnétique. C'est un ajout à la magnétostatique où le courant électrique est influencé par la variation temporelle de flux magnétique.

Planche 2 : Tout semble être dit dans la planche.

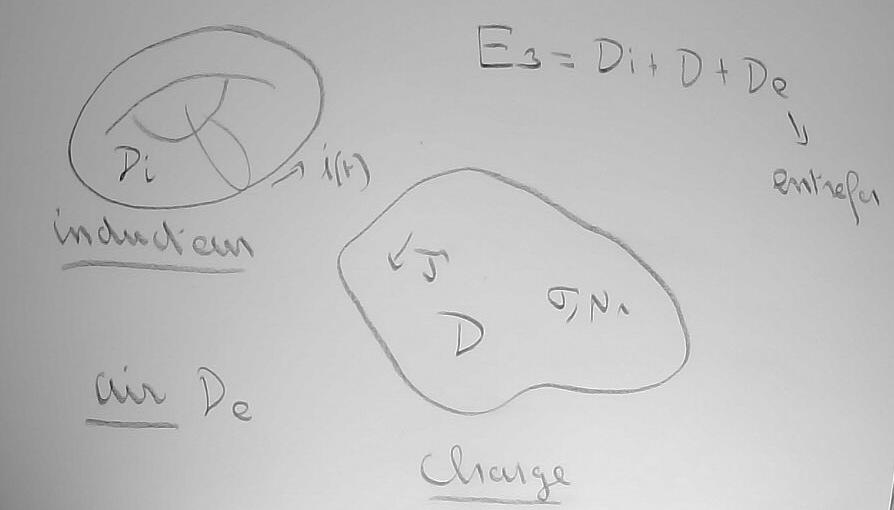
Planche 3 : La situation est celle du dessin ci-dessous

Il y a un domaine inducteur 'Di' : dans ce domaine circule un courant électrique 'i' qui dépend sinusoïdalement du temps et donc auquel on associe l'amplitude complexe 'i_barre' ;

il y a aussi un domaine 'D', appelé la charge, qui peut être le lieu de courants induits et donc est doté d'une conductivité 'sigma'. De plus il est doté d'une perméabilité magnétique relative 'mur'

et le reste de l'espace 'E3' est le domaine 'De' ('e' pour entrefer). C'est a priori de l'air mais en électrotechnique tout ce qui ne conduit pas le courant électrique ('sigma=0') et/ou qui n'est pas magnétique ('mur=1') est considéré comme de l'air. On dit aussi entrefer.

La question qui se pose est de calculer les courants induits (on dit aussi courants de Foucault) dans la charge.

Et comment utiliser ces courants induits pour calculer les densité de puissance Joule (la partie de la puissance qui contribue à chauffer la charge) et densité de forces d'origine électromagnétique dans cette charge.

Planche 4 : Voici les équations qui permettent de répondre à cette question.

On utilise directement le potentiel vecteur magnétique 'a' et, puique le courant inducteur depend sinusoïdalement du temps, on utilise même son amplitude complexe 'a_barre'. Ce faisant on néglige la phase transitoire nécessaire pour atteindre ce régime sinusoïdal établi (Approximation des Régimes Quasi-Stationnaire (ARQS) disent certains).

la conductivité 's' dans tout l'espace est une fonction constante par morceaux comme indiqué, ainsi que la perméabilité magnétique 'mu', ces grandeurs figurant dans l'équation dont le potentiel vecteur est l'inconnue.

Si la charge ne conduisait par l'électricité, cette équation serait celle de la magnétostatique (sans aimants) de la leçon précédente.

Mais comme elle conduit l'électricité, il est nécessaire d'y faire figurer la densité de courant induits qui est '-sigma (j omega a_barre + grad(phi_barre)' dans D et donc '-s (j omega a_barre + grad(phi_barre)' dans tout l'espace 'E3'

Pourquoi cette expression ? Le dessin ci-dessous y répond en bref

et on trouvera ici plus de détails.

On notera que 'phi_barre' est également une inconnue de l'équation, au même titre que 'a_barre' et on se souviendra que 'a_barre' n'est pas défini de façon unique. Ce qui fait qu'on peut jouer sur 'phi_barre' et 'a_barre' pour obtenir toute une famille d'équations dont certaines présentent plus d'avantages pratiques que d'autres.

Pour simplifier, on se limite en fait à un seul membre de la famille où : 'div(a_barre) =0' ; c'est une équation supplémentaire qui permet d'obtenir que 'phi_barre' soit défini de façon unique. En gros, on a comme champs scalaires inconnus les trois composantes de 'a_barre' et 'phi_barre' soit 4 inconnues scalaires qui doivent satisfaire 4 équations scalaires (les trois de 'rot(1/mu...' et 'div(a_barre)=0).

Il ne reste qu'à indiquer où se trouve le terme source de l'équation : c'est dans 'js_barre' qui représente la densité de courant dans l'inducteur qu'on va supposer connue (même si en fait l'inducteur est aussi le lieu de courants induits. Mais en première instance on peut ignorer cet aspect).

Planche 5 : Que fait-on de la solution de l'équation en supposant qu'elle soit résolue

On s'en sert déjà pour calculer la puissance réactive comme indiqué.

Planche 6 : Puis la densité de courants induits

Son examen permet d'inférer un mode de calcul de 'phi_barre' mais peu importe pour l'exploitation de la solution.

Planche 7 : Et finalement on calcule la puissance active qui, en l'absence de mouvement relatif entre l'inducteur et la charge, se limite à la puissance Joule.

Planche 8 : On sait donc que faire de la solution calculée, mais pour la calculer il faut que la densité de courant dans l'inducteur (le terme source de l'équation) soit spécifié.

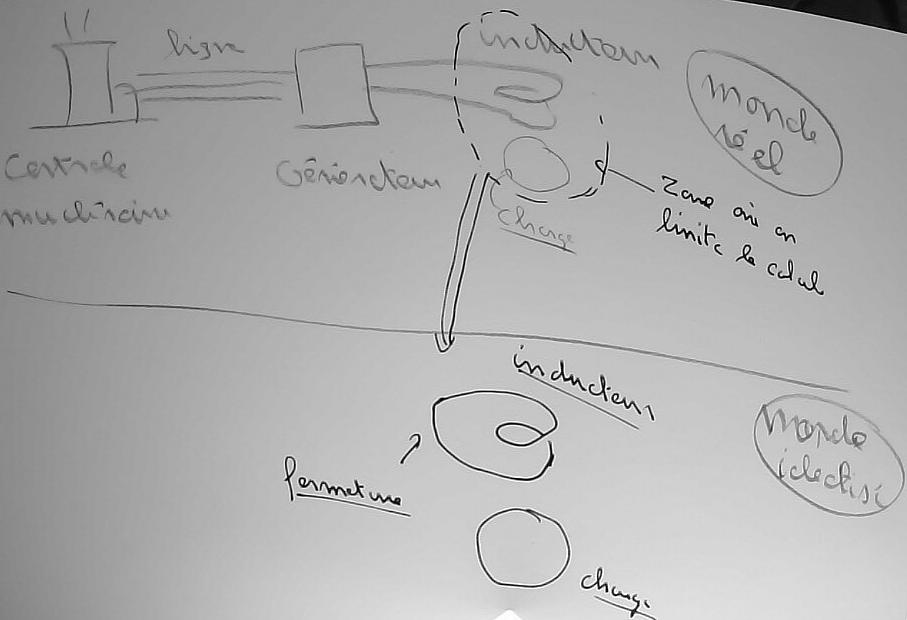
Un inducteur réel se présente comme sur la figure de la planche : une sorte de serpentin qui a deux extrémités par lesquel on le connecte à la source électrique qui l'alimente (le générateur).

L'inducteur du système d'équation de la planche 4 ne peut pas garder cette forme avec deux extrémités libres : où passerait le courant qui s'échappe par ces extrémités ? De plus les équations ne comportent aucun terme capable de prendre en compte le générateur.

Il va donc être nécessaire d'idéaliser l'inducteur réel pour qu'il puisse coïncider avec celui des équations.

Planche 9 : Cette idéalisation commence par la fermeture de l'inducteur sur lui même de façon qu'il n'ait plus d'extrémités libres. Le dessin ci-dessous tente de donner une idée de la situation.

Dans la réalité, il n'y a pas (sauf dans les condensateurs) de rupture des conducteurs par lesquels s'écoule le courant électrique. Une turbine dans une centrale nucléaire entraîne une sorte d'aimant (un électro-aimant), ce qui induit une force électromotrice dans les enroulements qui sont disposés à proximité de l'aimant en mouvement ; cette force électromotrice génère un courant qui est transporté par une ligne jusqu'à un générateur (je passe les multiples transformateurs) ; et le générateur recueille ce courant et le transforme en un courant à la fréquence ad hoc qui parcourt l'inducteur.

Mais pour éviter de décrire tout ces détails alors qu'on ne s'intéresse qu'à une petit zone de l'espace entier où résident tout ces éléments, il est nécessaire de limiter la zone dans laquelle se fait le calcul.

Aussi choisit-on d'approcher la configuration réelle par une autre où le courant dans l'inducteur est fermé sur lui-même.

Mathématiquement, ce courant fermé sur lui-même peut être séparé en un champ de vecteurs 'u' (le support du courant) nul en dehors de 'Di' et qui satisfait aux propriétés indiquées.

Et on procède ainsi parce que justement il existe un unique 'u' qui satisfait les propriétés. Il porte le (joli, si on apprécie un doigt de pédanterie) nom d'espace de cohomologie du tore, le tore étant le domaine torique formé par la fermeture de l'inducteur sur lui-même.

Planche 10 : Cette représentation du courant inducteur permet d'obtenir une expression pour le calcul de la tension 'v_barre' nécessaire pour faire circuler le courant inducteur. Celle qui est indiquée.

Et la légitimité de l'expression tient à ce qu'en manipulant les formes faibles de l'équation d'inconnues 'a_barre' en prenant en compte les propriété du support de courant inducteur 'u' on arrive à établir la relation fondamentale (cf. partie M. Dufour) : 'v_barre conjugué(i_barre) = P + j Q', 'P' et 'Q' étant les puissances active et réactive précédentes.

Le corollaire de ceci est qu'on peut obtenir une expression de l'impédance 'Z=v_barre / i_barre' du système inducteur+charge (en négligeant les pertes Joules dans l'inducteur, mais elles peuvent être prise en compte a posteriori).

Et c'est tout ce qui est utile pour dimensionner un dispositif d'induction électromagnétique.

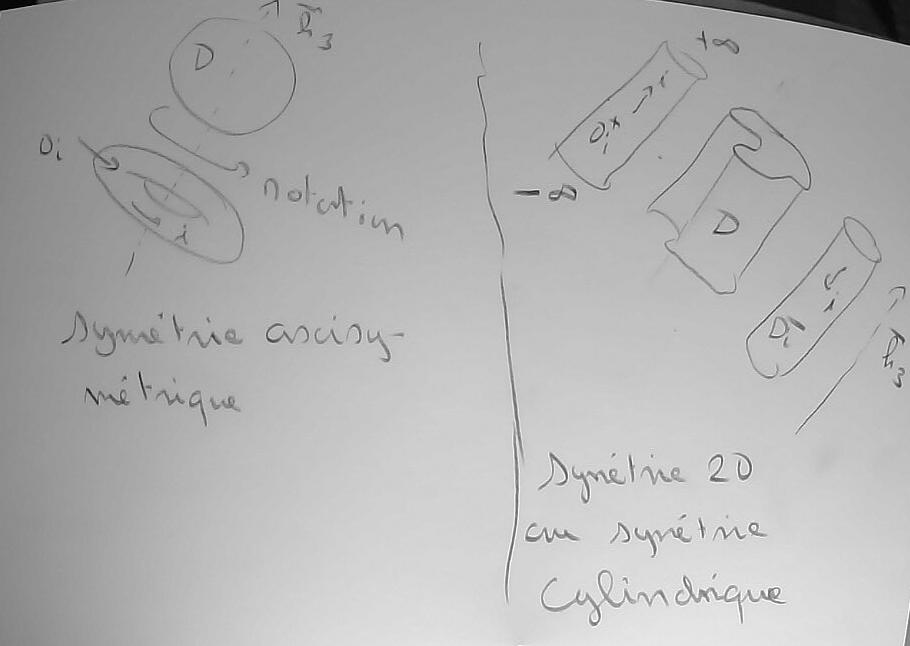
Intermède 1 : Jusqu'ici l'équation a été considérée en toute généralité. À partir d'ici elle va être appropriée aux cas de symétrie d'abord axisymétrique puis ensuite 2D droite.

La symétrie axisymétrique correspond au cas où des domaines inducteurs comme charge sont invariant dans une rotation autour d'un même axe.

De plus, le courant inducteur est supposé n'avoir de composante que la composante orthoradiale par rapport à cet axe

La symétrie 2D droite (ou symétrie cylindrique) correspond elle au cas où ces domaines sont invariants dans une translation dans une même direction.

De plus le domaine inducteur a au moins deux composantes connexes (il se présente en deux morceaux) ; dans l'un la densité de courant est dirigé suivant le vecteur directeur de la translation et dans l'autre dans le sens inverse.

On remarque que la symétrie axisymétrique a l'avantage d'être réalisable (correspondre à des objets réels), ce qui n'est pas le cas de la symétrie 2D droite.

C'est la raison pour laquel c'est la symétrie axisymétrique qui est traitée en premier, la symétrie 2D droite conduisant à des difficultés pour être connectée à aux objets réels.

Planche 11 : La position générale 'x' s'écrit en coordonnées cylindriques comme indiqué.

L'invariance géométrique par rapport à 'theta' permet déjà de décrire tout l'espace par le demi plan 'r kx + z kz' avec 'r>0'. Si 'r kx + z kz' est un point de D alors 'r ky + z kz' aussi comme d'ailleurs 'r (cos(alpha) kx + sin(alpha) ky) + z kz = x' pour 'alpha' quelconque.

De ce fait les fonctions de conductivité électrique et perméabilité magnétique s'expriment en coordonnées comme indiqué.

Et on peut changer de nom pour désigner 'D' qui est défini entièrement par 'Sigma' (le domaine de 'R+ x R' qu'est l'intersection de 'D' avec... disons le plan '(kx,kz)' mais ça pourrait être un plan quelconque pourvu qu'il soit méridional (i.e. passant par le méridien de la sphère de centre l'origine : '(cos(alpha) kx + sin(alpha) ky,kz)' pour 'alpha' quelconque)

Planche 12 : Comme indiqué précédemment on fait l'hypothèse que la densité de courant source n'a de composante que la composante orthoradiale par rapport à l'axe de symétrie : avec les coordonnées cylindriques, c'est facile à exprimer : 'js_barre_vecteur = js_barre_scalaire ktheta'.

Un examen des équations de la planche 4 amène à réduire le potentiel vecteur 'a_barre_vecteur' à sa simple composante orthoradiale 'a_barre' qui ne dépend que de 'r' et 'z'. Ce qui fait que l'équation se réduit considérablement à celle qui est indiquée.

Un fait notable est que le potentiel scalaire électrique 'phi_barre' disparaît de la modélisation. Pour expliquer en quoi c'est tout à fait normal, il aurait fallu aller plus loin dans l'analyse du modèle en 3D ; jusqu'à conférer à ce potentiel scalaire électrique le statut qui lui est dû, celui de prendre en compte les effets capacitifs en situation d'induction.

La symétrie axisymétrique permet de spécifier analytiquement l'élément générateur de l'espace de cohomologie de la planche 9. Il a la forme indiquée où 'Sigma_i' est à 'D_i' ce qu'est 'Sigma' à 'D'.

Planches 13 et 14 : et on peut également fournir les expressions des tensions sources, induction magnétique, puissances réactive et actives.

Comme l'équation permettant le calcul de 'a_barre' est tout à fait du genre de celles qui se calculent bien par éléments finis, on pourrait penser que tout est dit.

Mais il reste deux détails qui ont leur importance : d'abord le domaine de calcul est infini, ce qui suppose une troncature pour pouvoir utiliser des éléments finis (ou quelque chose de plus sophistiqué). M Dufour se charge d'expliquer cela.

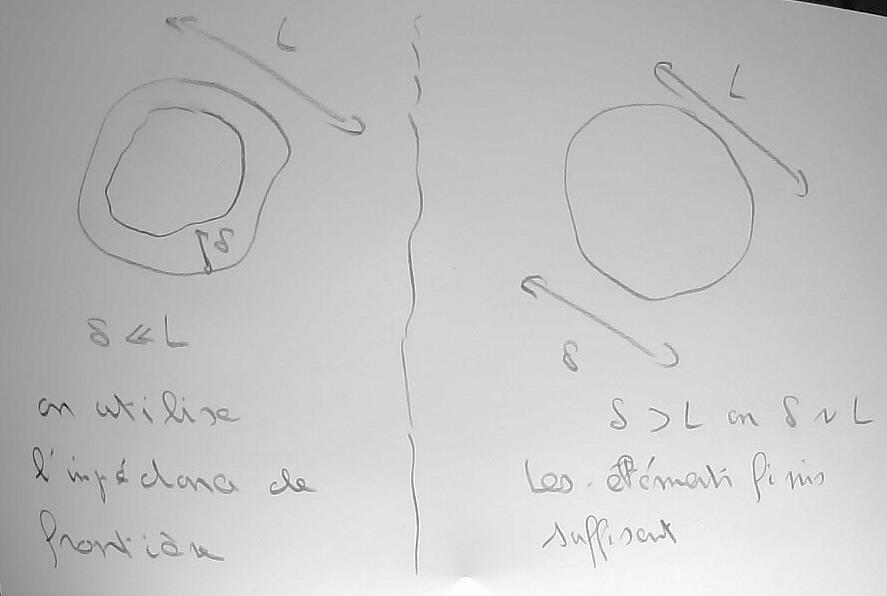
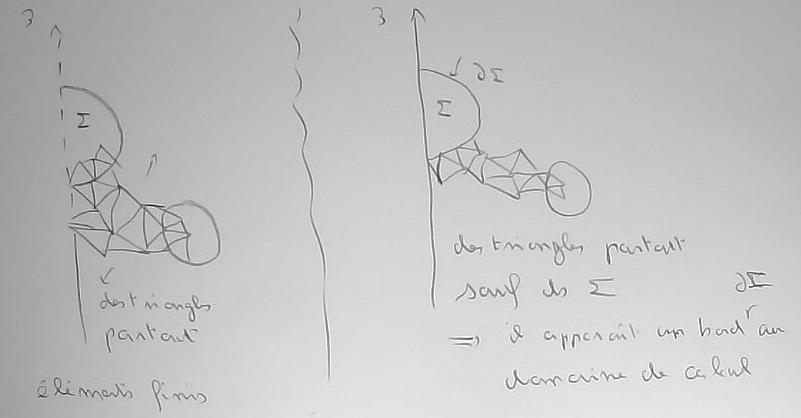
Ensuite, il se trouve que que les courants induits sont localisés au voisinage de la surface 'bord(D)' du domaine conducteur 'D', c'est à dire dans une une couche d'épaisseur le 'delta' qui est indiqué intérieure à ce bord.

Bien évidemment, cette description de la localisation des courants induits n'a de sens que lorsque la dimension caractéristique 'L' de 'D' est grande devant 'delta'.

Mais lorsque 'delta' est très inférieur à 'L' il devient problématique d'utiliser des 'eléments finis pour le calcul, comme expliqué dans dans la planche.

Pour ces cas (fréquents en chauffage par induction), on peut utiliser l'approximation de l'impédance de frontière.

Planche 15 : Le principe de l'approximation de l'impédance de calcul est illustré à un niveau pratico-pratique par le dessin ci-dessous

En passant les détails, on fait apparaître un bord suplémentaire dans le domaine de calcul et donc il faut disposer d'une condition aux limites pour 'a_barre' sur ce bord.

C'est celle qui est indiquée dans la planche.

Planche 16 : L'utilisation de l'approximation de l'impédance de frontière nécessite de modifier les expressions des puissance active et réactive comme indiqué. Le reste est inchangé.

Planches 17 à 22 : Maintenant tout ce qui a été dit dans le cas de la symétrie axisymétrique peut être, mutatis mutandis, redit dans le cas de la symétrique 2D droite.

C'est ce qui est fait dans les planches 17 à 22.

Planche 23 et suivantes : Pour bien vérifier que tout ce qui vient d'être dit est aussi bien compris, je vous propose cet exercice. Les planches suivantes en sont la correction.

La leçon est passée très vite sur certains détails de calculs qui sont mieux expliqués ici et là.