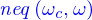Tout (v)oir /
(c)acher
sinon cliquer sur les items ci dessous pour voir/cacher individuellement leur contenu
Intentions de l'enseignement
Organisation de l'enseignement
Exemples de situations dotées d'objectifs
Traitements des exemples de situations
Rappels de cours
Tests
Intentions de l'enseignement
Comme le titre l'indique, il s'agit d'apprendre à poser et résoudre un problème.
De quels problèmes s'agit-il ?
Les problèmes dont il s'agit se posent donc en termes d'exposé d'une situation dans laquelle on cherche à atteindre un objectif.
Et l'objectif s'atteint en passant par la résolution d'un problème mathématique.
Pour le problème de dimensionnement du câble en antartique, il y a l'échauffement par unité de longueur lorsque le courant est maximal 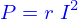 pour
pour  et où
et où  est la résistance électrique par unité de longueur du câble ; la température maximale que peut admettre l'isolant électrique ; la température la plus chaude qui peut être atteinte en antartique ; et un modèle de transfert de chaleur dans la section du câble qui dépend de l'agencement du conducteur en cuivre et de l'isolant dans le câble.
est la résistance électrique par unité de longueur du câble ; la température maximale que peut admettre l'isolant électrique ; la température la plus chaude qui peut être atteinte en antartique ; et un modèle de transfert de chaleur dans la section du câble qui dépend de l'agencement du conducteur en cuivre et de l'isolant dans le câble.
Par ailleurs, il y a une certaine inconscience à prétendre apprendre à poser er résoudre un problème.
L'un des premiers qui s'y est essayé est Descartes dans son Discours de la méthode
Et pour montrer que ce qu'il raconte dans ce discours n'est pas du verbiage, il le présente comme une introduction à une série de traités sur divers sujets dont l'un est le texte fondateur de notre géométrie analytique.
Donc pourquoi les règles de Descartes ne suffiraient-elles pas ?
La réponse est pragmatique : elles ne suffisent pas en elles-même. Il est de plus nécessaire de pratiquer cette activité qui consiste à poser et résoudre des problèmes pour se convaincre qu'on sait à peu près le faire.
Et c'est ce que couvre l'enseignement. On va énumérer un certain nombre de situations dans lesquelles il s'agira d'atteindre un objectif. Il faudra transformer cela en problèmes puis les résoudre.
L'intitulé de l'enseignement vient d'un livre écrit par George Polya Comment poser et résoudre un problème dont on va s'efforcer de suivre les conseils
Organisation
Il est prévu 7 séances (de 1.25h) de CM, 7 séances (de 1.25h) de TDs et 2 séances de tests (de 1.25h).
Elles seront remplies ainsi : tout d'abord, nous aurons une lecture commune assez rapide de l'ensemble des situations posées dans la section suivante.
Puis nous traiterons ces situations une à une.
Le traitement donnera lieu à des rappels de cours à propos des thèmes abordés, celui-ci pouvant être fait avant ou après le traitement de chaque situation, selon les cas.
Il y aura peut-être quelques extensions dans les rappels de cours, mais le moins possible. L'objectif étant de faire en sorte que vous mobilisiez les connaissances que vous avez déjà.
Les traitement des situations et les rappels de cours seront insérés dans cette page au fur et à mesure de l'avancement de l'enseignement ; celle-ci n'est donc pas statique.
Exemples de situations dotées d'objectifs
Voici une suite de situations qui n'est ni exhaustive de ce qui peut être rencontré, ni complète. Elles seront complétées au fur et à mesure de l'avancée de l'enseignement.
Situations algébriques
Typiquement : J'ai le double de l'âge que tu avais quand j'avais ton âge. Quand tu auras mon âge, ensemble nous aurons 63 ans.
Et encore : (même s'il s'agit plus d'un problème qu'on classe en analyse plutôt qu'en algèbre) Le professeur de thermodynamique dit que lorsque P, V et T sont liés par une loi d'état alors
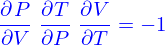 .
Comment le justifier ?
.
Comment le justifier ?
Situations géométriques
Typiquement : retrouver les sinus et cosinus du double d'un angle en fonction de ceux de l'angle simple.
Encore : le problème de Kepler sur la question de la mesure du volume des tonneaux de vin
Et encore : Trouver la forme de l'ombre portée sur le sol considéré comme un plan par un dirigeable dont la forme est ellipsoïdal. Lorsque la source de la lumière est le soleil, lorsqu'elle est une source ponctuelle (située au dessus de l'ellipsoïde : par exemple embarquée dans un hélicoptère).
Situations cinématiques.
Typiquement : Comment aller d'une position située d'un côté d'une rivière à une position qui est située de l'autre côté en temps minimal sachant qu'on marche à la vitesse 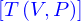 sur terre et qu'on nage à la vitesse
sur terre et qu'on nage à la vitesse  .
.
On peut compliquer le problème en supposant que l'eau de la rivière (supposée être une sorte de canal rectiligne de largeur  ) s'écoule à la vitesse (uniforme)
) s'écoule à la vitesse (uniforme)  .
.
Situations impliquant des connaissances de physique
Typiquement : Expliquer le principe du niveau à bulle : ceci et cela.
Et faire les calculs utiles à la fabrication de cet objet.
Encore : Une boule de billard se déplaçant en ligne droite vient percuter une autre boule qui était immobile. Quel est le mouvement des deux boules après le choc ?
Et encore : Une balle en caoutchouc est lancée. Elle effectue une série de rebonds de plus en plus petits jusqu'à rouler sur le sol. Expliquer cela. Quel modèle peut-il rendre compte de ce qu'on observe ?
Situation probabilistes
Typiquement : Un joueur est placé devant trois portes fermées. Derrière l'une d'elles
se trouve une voiture et derrière chacune des deux autres se trouve une chèvre. Il doit tout d'abord désigner une porte. Puis le présentateur ouvre une porte qui n'est ni celle choisie par le candidat, ni celle cachant la voiture (le présentateur sait quelle est la bonne porte dès le début). Le candidat a alors le droit ou bien d'ouvrir la porte qu'il a choisie initialement, ou bien d'ouvrir la troisième porte. (problème de Monty Hall)
Quelle est la meilleure tactique que le joueur puisse adopter ? (pour gagner la voiture, pas une chèvre)
Lorsque ce problème est résolu, il n'y a plus de difficultés pour considérer un problème analogue avec un nombre de portes quelconque (1 seule voiture et le reste en chèvres). Le faire.
Situations logiques
Typiquement : Ce genre de questions
Mais c'est mieux quand c'est une vraie liste d'exercice de cours de logique !
Exo 66 -- solution juste
Exo 66 -- solution fausse Exo 65
ou celui-ci
Rappels de cours
Nombres complexes (in a nutshell)
Un nombre complexe est une expression de la forme
où 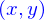 sont des nombres réels ordinaire mais où
sont des nombres réels ordinaire mais où  est une solution de l'équation
comme il semblait bizarre d'emblée de supposer que le carré de quelque chose soit négatif, on a appelé les quelque choses en question des « nombres imaginaires. » Leur intérêt étaient qu'il permettaient de réaliser des calculs (avec
est une solution de l'équation
comme il semblait bizarre d'emblée de supposer que le carré de quelque chose soit négatif, on a appelé les quelque choses en question des « nombres imaginaires. » Leur intérêt étaient qu'il permettaient de réaliser des calculs (avec  comme seule modification de l'algèbre utilisée) et de produire des résultats tout à fait cohérents.
comme seule modification de l'algèbre utilisée) et de produire des résultats tout à fait cohérents.
Cet aspect bizarre a disparu dès lors qu'on s'est rendu compte que cette expression pouvait 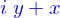 était une notation algébrique qui représente bien un vecteur du plan euclidien qui a pour coordonnées
était une notation algébrique qui représente bien un vecteur du plan euclidien qui a pour coordonnées 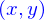 dans une base orthonormée.
dans une base orthonormée.
L'ensemble des nombres complexes est donc isomorphe au plan euclidien. Ce plan est appelé le plan d'Argand.
Cette appellation d'imaginaire est tombé en quasi désuétude à ceci près qu'on appelle parties réelle et imaginaire
Les additions, soustraction, multiplication et division de deux nombres complexes sont (on introduit 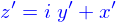 )
)
On remarque que pour la division 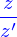 , on a mis le résultat sous la forme de la somme d'une partie réelle et d'une partie imaginaire multiplié par
, on a mis le résultat sous la forme de la somme d'une partie réelle et d'une partie imaginaire multiplié par  . Cette réduction particulière (comme d'ailleurs bien d'autres) se fait aisément si on introduit l'opération de conjugaison complexe (notée par une étoile en exposant du symbole avec lequel le nombre complexe est noté)
. Cette réduction particulière (comme d'ailleurs bien d'autres) se fait aisément si on introduit l'opération de conjugaison complexe (notée par une étoile en exposant du symbole avec lequel le nombre complexe est noté)
On a alors un premier résultat
où on remarque alors que le produit d'un complexe par son conjugué est la carré de la norme du vecteur qui lui est associé dans le plan d'Argand.
On convient d'appeler module (notée par des barres de chaque côté du symbole avec lequel le nombre complexe est noté)
La mise en forme de la division de deux complexes se fait alors comme
L'introduction de la conjugaison complexe permet également d'associer des expressions algébriques à la prise de parties réelle et imaginaire
Les nombres complexes peuvent être exprimés sous forme polaire, soit
où 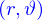 sont tels que
sont tels que
on a bien sûr 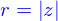 et il est un peu plus difficile d'obtenir
et il est un peu plus difficile d'obtenir 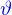 , mais ce n'est souvent pas nécessaire.
, mais ce n'est souvent pas nécessaire.  est le module de
est le module de  et on appelle
et on appelle 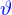 son argument.
son argument.
Les fonctions de variables complexes sont obtenues par leur définition sous forme de séries entières. Ainsi l'exponentielle est la fonction telle que (rayon de convergence infini)
on a alors
comme on peut définir les  et
et  par leurs séries
on obtient que
par leurs séries
on obtient que
Comme la plupart des propriétés de l'exponentielle, notamment
restent valables pour les complexes, on peut déduire que
c'est la formule de Moivre.
Quelques exercices
- On n'a pas insisté sur l'association entre nombres complexes et vecteur du plan euclidien qu'il représente. Examiner géométriquement à quoi correspondent les relations algébriques établies.
- Pour un nombre entier
 qulconque, chercher les racines de l'unité, soit résoudre
qulconque, chercher les racines de l'unité, soit résoudre
Fonctions de plusieurs variables (in a nutshell)
Équations différentielles ordinaires (in a nutshell)
Si on donne une fonction
qu'on la choisisse continue pour tout  , i.e.
et différentiable, toujours pour tout
, i.e.
et différentiable, toujours pour tout  , i.e. la limite
existe toujours et alors on appelle dérivée de
, i.e. la limite
existe toujours et alors on appelle dérivée de  la fonction
la fonction
Une telle fonction peut être spécifiée par des conditions de la forme
où 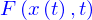 est une expression algébrique quelconque de
est une expression algébrique quelconque de 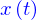 et
et  On dit que cette expression est une équation différentielle ordinaire (EDO) d'ordre 1 (parce qu'elle ne fait intervenir que la dérivée première de
On dit que cette expression est une équation différentielle ordinaire (EDO) d'ordre 1 (parce qu'elle ne fait intervenir que la dérivée première de  ) dont l'inconnue est la fonction
) dont l'inconnue est la fonction  .
.
Si la fonction  est choisie de manière que sa dérivée est elle-même continue et différentiable, on appelle dérivée seconde de
est choisie de manière que sa dérivée est elle-même continue et différentiable, on appelle dérivée seconde de  la fonction
la fonction
On peut former une équation différentielle d'ordre 2, en demandant que la fonction  satisfasse à la relation
satisfasse à la relation
où 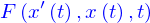 est une expression algébrique quelconque de
est une expression algébrique quelconque de 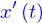 ,
, 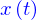 et
et  .
.
On ne sait pas en général résoudre les EDOs. Par contre on sait en résoudre certaines dont il est utile de connaître la forme des solutions.
Voici les incontournables !
EDO d'ordre 1 à variables séparables
C'est
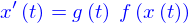
les solutions ont la forme
EDO d'ordre 2 à coefficients constants sans second membre
C'est
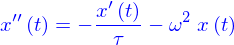
il y a trois cas. On pose
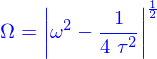
Si 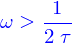 les solutions sont de la forme
les solutions sont de la forme
Si 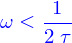 les solutions sont de la forme
les solutions sont de la forme
Si 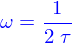 les solutions sont de la forme
les solutions sont de la forme
EDO d'ordre 2 à coefficients constants avec second membre
C'est 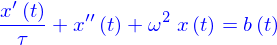
Les solutions sont la somme des solutions sans le second membre 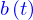 et d'une solution particulière. de l'équation.
et d'une solution particulière. de l'équation.
Pour trouver celle-ci simplement, il est préférable de transformer l'EDO de second ordre d'une variable scalaire en EDO du premier ordre d'une variable vectorielle. Mais je pense que vous n'avez pas vu cela, qui est raconté ici.
Aussi va-t'on se limiter au cas oscillant.
EDO d'ordre 2 à coefficients constants avec second membre oscillant
où 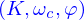 sont des constantes, avec
sont des constantes, avec 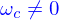
La solution particulière est alors
Si  , on pose
, on pose
puis on introduit  tel que
et alors
tel que
et alors
Si 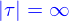 , il y a deux cas.
, il y a deux cas.
Si 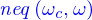
Quelques éléments de logique
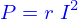 pour
pour  et où
et où  est la résistance électrique par unité de longueur du câble ; la température maximale que peut admettre l'isolant électrique ; la température la plus chaude qui peut être atteinte en antartique ; et un modèle de transfert de chaleur dans la section du câble qui dépend de l'agencement du conducteur en cuivre et de l'isolant dans le câble.
est la résistance électrique par unité de longueur du câble ; la température maximale que peut admettre l'isolant électrique ; la température la plus chaude qui peut être atteinte en antartique ; et un modèle de transfert de chaleur dans la section du câble qui dépend de l'agencement du conducteur en cuivre et de l'isolant dans le câble.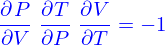 .
Comment le justifier ?
.
Comment le justifier ?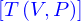 sur terre et qu'on nage à la vitesse
sur terre et qu'on nage à la vitesse  .
. ) s'écoule à la vitesse (uniforme)
) s'écoule à la vitesse (uniforme)  .
. 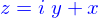
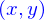 sont des nombres réels ordinaire mais où
sont des nombres réels ordinaire mais où  est une solution de l'équation
est une solution de l'équation
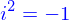
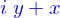 était une notation algébrique qui représente bien un vecteur du plan euclidien qui a pour coordonnées
était une notation algébrique qui représente bien un vecteur du plan euclidien qui a pour coordonnées 
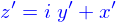 )
)
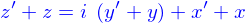
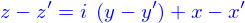
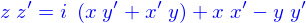
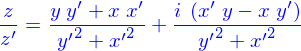
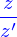 , on a mis le résultat sous la forme de la somme d'une partie réelle et d'une partie imaginaire multiplié par
, on a mis le résultat sous la forme de la somme d'une partie réelle et d'une partie imaginaire multiplié par  . Cette réduction particulière (comme d'ailleurs bien d'autres) se fait aisément si on introduit l'opération de conjugaison complexe (notée par une étoile en exposant du symbole avec lequel le nombre complexe est noté)
. Cette réduction particulière (comme d'ailleurs bien d'autres) se fait aisément si on introduit l'opération de conjugaison complexe (notée par une étoile en exposant du symbole avec lequel le nombre complexe est noté)

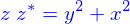
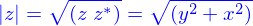
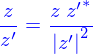
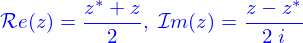
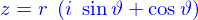
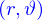 sont tels que
sont tels que
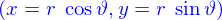
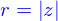 et il est un peu plus difficile d'obtenir
et il est un peu plus difficile d'obtenir 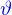 , mais ce n'est souvent pas nécessaire.
, mais ce n'est souvent pas nécessaire.  est le module de
est le module de  et on appelle
et on appelle 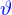 son argument.
son argument.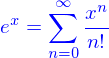

 et
et  par leurs séries
par leurs séries
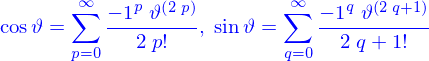
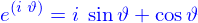

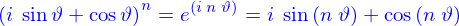
 qulconque, chercher les racines de l'unité, soit résoudre
qulconque, chercher les racines de l'unité, soit résoudre
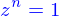
 est une expression de calcul qui a une valeur qui dépend de
est une expression de calcul qui a une valeur qui dépend de  et
et 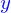 .
.
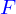 .
.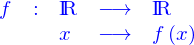
 est
est
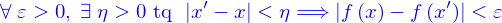
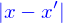 .
.
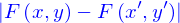 aussi petite qu'on veut en jouant sur la distance entre
aussi petite qu'on veut en jouant sur la distance entre 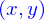 et
et 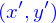 .
.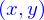 et les
et les 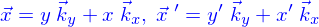
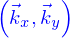 .
.
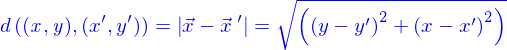
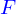 se décalcque tout naturellement comme
se décalcque tout naturellement comme
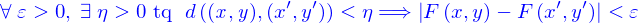
 correspond à l'existence de la limite
correspond à l'existence de la limite
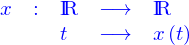
 , i.e.
, i.e.
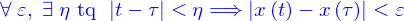
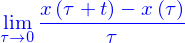
 la fonction
la fonction
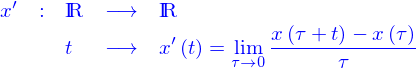
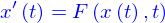
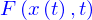 est une expression algébrique quelconque de
est une expression algébrique quelconque de 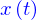 et
et  On dit que cette expression est une équation différentielle ordinaire (EDO) d'ordre 1 (parce qu'elle ne fait intervenir que la dérivée première de
On dit que cette expression est une équation différentielle ordinaire (EDO) d'ordre 1 (parce qu'elle ne fait intervenir que la dérivée première de  ) dont l'inconnue est la fonction
) dont l'inconnue est la fonction  .
.
 est choisie de manière que sa dérivée est elle-même continue et différentiable, on appelle dérivée seconde de
est choisie de manière que sa dérivée est elle-même continue et différentiable, on appelle dérivée seconde de  la fonction
la fonction
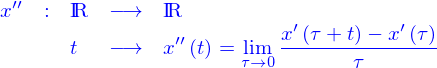
 satisfasse à la relation
satisfasse à la relation
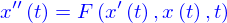
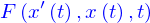 est une expression algébrique quelconque de
est une expression algébrique quelconque de 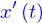 ,
, 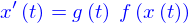
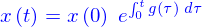
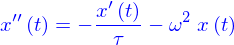
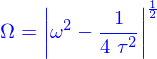
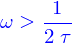 les solutions sont de la forme
les solutions sont de la forme
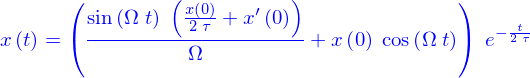
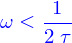 les solutions sont de la forme
les solutions sont de la forme
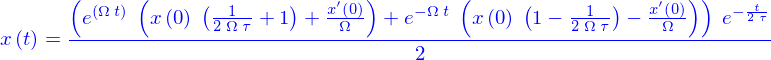
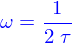 les solutions sont de la forme
les solutions sont de la forme

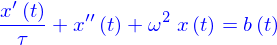
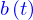 et d'une solution particulière. de l'équation.
et d'une solution particulière. de l'équation.

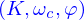 sont des constantes, avec
sont des constantes, avec 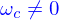
 , on pose
, on pose
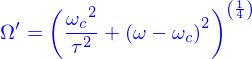
 tel que
tel que
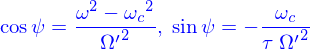

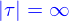 , il y a deux cas.
, il y a deux cas.