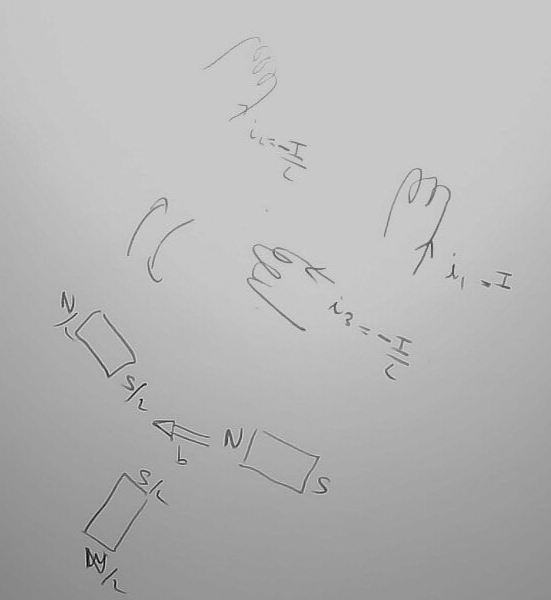Planche 1 : La leçon sur la machine asynchrone a eu lieu la semaine dernière. C'est un convertisseur électromécanique. Mais la présentation qui en a été faite a mis l'accent sur la représentation externe de ce convertisseur. Le modèle d'EDOs (Équations Différentielles Ordinaires) de la machine asynchrone a été donné et toute la leçon a été consacrée à l'étude de ce modèle.

Cette leçon porte sur les convertisseurs électromécaniques qui ne nécessitent pas la présence de courants induits pour fonctionner. Alors que leur présence est l'ingrédient essentiel de la machine asynchrone (elle s'appelle, dans sa version moteur, induction motor pour les anglo-saxons).

Du point de vue de l'électromagnétisme, l'analyse des situations où il y a des courants induits est un peu plus difficile que celles où ils sont absents. Et c'est pourquoi la machine asynchrone a été présentée ainsi.

Les convertisseurs dont le fonctionnement ne repose pas sur ces courants induits, par contre, pourraient presque être être introduits à partir du point de vue de l'électromagnétisme qui se limiterait à la magnétostatique.

Mais presque seulement. Parce qu'il faudrait convoquer l'outillage conceptuel des champs de vecteurs dans tout l'espace et de leurs propriétés. Ce qui prendrait un temps dont nous ne disposons pas.

J'ai donc choisi une méthode de présentation de moyen terme qui ne nécessite comme pré-requis que l'électromagnétisme approprié aux connaissances mathématiques de 1ier cycle.

Planche 2 : Quels sont les objectifs de la leçon ?

Tout d'abord, la question du couplage entre l'électricité et la mécanique va être décrite sur l'exemple de ce qu'on appelle le cadre tourtnant.

Cette description à laquelle on ajoute celle des contacts glissants permet alors d'établir les équations des machines synchrones. La machine à courant continu étant considérée comme telle, bien qu'elle ne le soit pas dans un sens strict. En fait une meilleure dénomination serait machine hamiltonienne mais comme ce n'est pas dans le vocabulaire courant de l'électrotechnique, nous ne l'utiliserons pas.

Puis quelques éléments sur un approche synthétique de l'électromécanique seront fournis.

Planche 3 : On part d'un fil de cuivre fermé sur lui-même et qui a la géométrie d'un rectangle, ce qu'on appelle un cadre.

Ce cadre est supposé ne pouvoir se déplacer qu'en rotation autour de l'un de ces deux axes de symétrie. Et on note 'Theta' L'angle qu'il fait avec un plan donné, qu'on appelle le plan de référence. Comme le cadre peut tourner sur lui-même 'Theta' est une variable dépendante du temps, et sa dérivée temporelle (la vitesse angulaire) est notée 'Omega'. (La notation pour la dérivée temporelle est celle de Newton)

Autour du cadre, on suppose qu'il y a une induction magnétique uniforme (c'est à dire constante dans tout l'espace) 'b' dirigée suivant la normale au plan par rapport auquel est repérée l'angle 'Theta'.

L'électromagnétisme élémentaire de 1ier cycle nous dit alors que : le flux magnétique dans le cadre est 'b cos(Theta) S' où 'S' est la surface du cadre et donc 'S cos(Theta)' est la surface projetée sur le plan de référence ; la variation temporelle de ce flux magnétique génère dans le cadre une force électromotrice qui est la dérivée temporelle du flux magnétique (loi de Faraday).

Si la matière dont est composé le cadre est un conducteur de l'électricité, il y aura donc un courant électrique 'i' qui parcourt le cadre. Ce courant électrique doit équilibrer la force électromotrice. Pour cela il y a deux contributions :

- La résistance électrique 'r' du cadre, qui correspond à une chute de tension 'r i' ;

- L'inductance propre 'l' du cadre pour laquelle la chute de tension est 'l di/dt'. (on utilise la notation de Leibnitz pour la dérivée temporelle parce qu'il n'est pas très lisible de mettre un point sur un 'i').

d'où la relation du bas de la planche. On l'appelle l'équation électrique.

Planche 4 : Cette équation électrique permet de connaître le courant qui parcourt le cadre quand on connaît son mouvement, i.e. la dépendance 'Theta' en temps.

Il faut maintenant trouver une équation qui permet de trouver le mouvement du cadre quand on connaît le courant qui le parcourt. Ce sera l'équation mécanique.

Elle sera de la forme : moment d'inertie du cadre x accélération angulaire = somme des couples s'exerçant sur le cadre.

Et donc, ce qu'il faut chercher c'est le couple d'origine électromagnétique (couple électromagnétique en bref) que cette situation génère.

Pour cela on part (toujours cf. électromagnétisme élémentaire), de l'expression de la force de Laplace sur un courant. Pour un « segment rectiligne de courant » (cette notion n'est pas heureuse parce qu'il n'y a pas de segments de courant qui peuvent exister seuls dans tout l'espace mais seulement une suite de segments qui forment un circuit fermé sur lui-même) c'est :

- En intensité : 'intensité du courant' x 'composante de l'induction magnétique dans le plan normal à la direction du segment' ;

- En direction : la direction normale au plan formé par la direction du segment et celle de l'induction magnétique, avec un sens qui se retrouve avec la règle du tire-bouchon, des trois doigts ou toute autre considération de ce genre.

On arrive donc à la formule de couple indiquée sur la planche. Et à l'équation mécanique juste en dessous.

Planche 5 : Ces équations forment le système dynamique du mouvement du cadre, qui peut être résolu (numériquement) dès lors qu'on lui ajoute des conditions initiales sur 'i', 'Theta' et 'Omega'.

Mais on peut aussi chercher des invariants au système. Sans la résistance électrique et si le couple extérieur était nul, on trouverait comme invariant la somme des énergies magnétique et cinétique.

On sait que l'énergie cinétique est '1/2 J Omega^2' mais on connait moins bien a priori l'expression de l'énergie magnétique. Ce n'est pas gênant parce que le système dynamique contient toute l'information au prix d'une manipulation.

Cette manipulation est faite en haut de la planche : on multiplie l'équation électrique par 'i', l'équation mécanique par 'Omega' et, compte tenu que 'i l di/dt = d/dt( 1/2 l i^2)' ainsi que 'Omega J dOmega/dt = d/dt ( 1/2 J Omega^2)' (ce qui se voit pas simple inspection des relations), on arrive à la relation du milieu de la planche.

Qu'a-t'on fait ? On a éliminé entre les deux relations (électrique et mécanique) un terme qui leur était commun '- b S i Omega sin(Theta)'. Et on a obtenu une expression dans laquelle les termes sont physiquement identifiables.

Il y a 'r i^i' c'est 'i' multiplié par 'r i' qui est la chute de tension au passage d'un courant 'i' dans la résistance 'r' ; ce terme est la puissance instantanée dissipée dans la résistance.

Il y a aussi 'Gamma_x Omega', c'est, en valeur absolue, la puissance injectée au phénomène qui crée le couple extérieur (typiquement du frottement) quand la vitesse est 'Omega'.

Et donc le terme '1/2 J Omega^2 + 1/2 l i^2' est l'énergie du cadre parcouru par un courant 'i' et tournant à la vitesse 'Omega' dont la variation est la source des puissances précédentes. On n'est pas surpris par le terme cinétique, ni d'ailleurs par le terme électrique mais c'est toujours aussi bien de le trouver dans le système dynamique plutôt que de le parachuter a priori.

On peut aussi examiner le terme qui est éliminé dans l'addition des bilans de puissances (les remarques précédentes justifient cette appellation). C'est '- b S i Omega sin(Theta)' qui est donc tel qu'il joue positivement dans un des bilan et négativement dans l'autre : c'est la puissance échangé entre l'électricité et la mécanique. Le terme d'interaction !

On remarque que si 'i=0' il n'y a pas de puissance échangée. Un cadre en bois (de résistance électrique infinie) peut tourner dans un champ magnétique sans qu'il y ait production de couple de nature électrique.

De la même façon, si 'Omega =0' il n'y a pas de puissance échangée. Aucun courant électrique n'est généré dans un cadre en cuivre immobile dans un champ magnétique.

Planche 6 : Voyons maintenant ce qu'on tirer de l'analyse précédente comme conséquence pratique.

On suppose que le cadre peut tourner librement sans aucun frottement. Il vient alors que la quantité '1/2 J Omega^2 + 1/2 l i^2' (l'énergie totale : électrique + mécanique) est décroissante dans le temps tant que 'i' n'est pas nul.

Comme c'est une quantité positive, qu'on sait bien qu'une fonction positive et décroissante a une limite inférieure, qu'il faut que 'i' soit nul pour que la quantité ne soit plus strictement décroissante, il vient alors la conclusion indiquée.

Le cadre tournant n'a pas une fonction de moteur mais plutot de frein.

Si on veut avoir un moteur ou un générateur il faut changer les conditions données.Et il y a deux possibilité pour cela :

- faire tourner l'induction 'b' conjointement au cadre ;

- apporter une force électromotrice extérieure dans le circuit du cadre.

Planche 7 : Tout d'abord l'apport de la force électromotrice extérieure.

Cela suppose d'ouvrir le cadre et d'ajouter cette force électromotrice par cette ouverture.

Mais le cadre tourne et on ne veut pas que la force électromotrice tourne avec lui.

On peut alors pratiquer l'ouverture comme indiqué par le dessin : c'est un contact glissant.

Et après avoir réalisé ce contact glissant, l'équation électrique de vient celle qui est indiquée dans la planche.

Une force électromotrice 'e_x' s'y ajoute. Celle-ci est fournie par un dispositif extérieur et elle peut être réglée, on dit plutôt contrôlée. Comment doit-elle l'être pour obtenir par exemple une fonction de moteur ?

Eh bien de telle manière que le couple électromagnétique soit toujours positif.

Il existe un discipline qui s'intéresse à chercher la forme de la source (ici 'e_x' comme fonction du temps) qui, compte tenu de contraintes (pratiquement, on ne peut pas réaliser n'importe quel 'e_x'), fait qu'une quantité qui est calculée via un système différentiel (les équations électrique et mécanique) soit la plus grande possible (ici on prendra pour quantité la moyenne temporelle de 'Gamma' après avoir limité le choix de 'e_x' à celui des fonction périodiques).

Cette discipline s'appelle le contrôle optimal (la source dont il est question s'appelle la commande et la quantité à maximiser la fonction objectif).

Il est hors de question de faire ici une longue disgression sur les méthodes du contrôle optimal pour traiter le cas particulier qui nous intéresse.

Aussi se limite-t'on à donner les conclusions qu'apporteraient cette étude.

Celles-ci sont que le 'e_x' qui maximise la valeur moyenne du couple doit être une fonction discontinue et constante par morceaux.

Planche 8 : Pratiquement, cette tension discontinue et constante par morceaux est obtenue par commutation.

La commutation peut être réalisée par de l'électronique de puissance avec les composants décrits leçon no3 ; on parle alors de commutation électronique. Nous n'allons pas nous occuper de la commutation électronique.

Et elle peut être réalisée mécaniquement. Pour cela on transforme les deux bagues du contact glissant en une seule bague coupée longitudinalement comme sur le dessin.

On voit que le circuit constitué par le cadre est alors soumis à une tension source 'e_x' (ou force électromotrice) qui est soit 'V' soit '-V'.

Et 'e_x' dépend donc de la position angulaire 'Theta' du cadre. L'angle 'Theta_x' prend en compte que la position des contacts qui frottent sur la bague coupée peut être réglée également en angle.

On arrive alors à la forme indiquée pour 'e_x' où 'Pi' est la fonction qui vaut 1 quand son argument est positif et -1 sinon.

Planche 9 : Tous les éléments sont en place pour fournir un 1ier modèle pour le cadre tournant dans un champ magnétique uniforme lorsque ce cadre est reliée à un collecteur (c'est le nom de la bague coupée).

Ce modèle permet de décrire la dynamique du mouvement du cadre. Mais en premier lieu il est intéressant d'examiner s'il permet un mouvement de rotation uniforme ('Omega' = constante => 'Theta = Omega t + Theta_0') pour un 'Gamma_x' lui aussi constant.

On voit facilement que ça ne marche pas puisque la 1ière équation dont la variable dépendante est 'i' montre que 'i' ne peut pas être constant.

Par contre on peut se livrer à une analyse plus ou moins convainquante comme celle de la page 4 du chapitre 5 du polycopié pour arriver à ce qui suit.

Plutôt que de considérer 'i' (le courant dans le cadre) on considère 'I' le courant dans le circuit extérieur au cadre.

On accepte qu'une fonction sinusoïdale est très proche de la fonction créneau obtenue avec elle ('sin(Theta) = Pi(sin(Theta))')

Et alors, en négligeant les termes en 'd/dt' il vient les relations indiquées en milieu de panche, où 'Gamma' est le couple électromagnétique qui doit s'équilibrer avec le couple extérieur 'Gamma_x' ('Gamma = Gamma_x')

On a obtenu les équations de la machine à courant continu.

Bien sûr, on a été très vite pour décrire les approximations. En fait une (plus précise mais plus longue) façon de procéder aurait été de poser 'i = I_constant Pi(sin(Theta)) + delta i', 'Omega = Omega_constant + delta Omega' 'Theta = Omega_constant t + delta Theta' ; de chercher de quelles équations sont solutions les grandeurs en 'delta' ; de vérifier que ces solutions de ces équation (pour des valeurs bien choisies de 'I_constant, Omega_constant') avaient des valeurs faibles devant ces 'I_constant, Omega_constant'.

En somme de procéder par perturbation.

Mais cette étude aurait amenées les même conclusion.

Planche 10 : Les machines à courant continue réelles sont plus compliquées que la cadre tournant.

Elles sont en fait composée d'un enroulement complexe qui se révèle fonctionner comme un cadre tournant. Pour cela la collection (par le collecteur) des courants dans le passage entre la partie tournant (le rotor) et la source de tension qui l'aliment se fait via un collecteur bien plus compliqué.

De plus l'induction uniforme 'b' est créée par d'autres enroulements disposés sur une carcasse magnétique qui ont pour effet de créer un induction magnétique uniforme (pour les machines bipolaires) juste à l'endroit où se trouve le rotor.

Il n'empêche que les équations obtenues pour le cadre tournant simple restent valables.

Elle sont cependant présentées de manière un peu différent. Comme celle qui est indiquée.

Pour le dessin : le circuit de gauche représente le stator (qu'on appelle l'inducteur) ; le circuit de droite (le cercle avec deux fils) représente le rotor (qu'on appelle l'induit).

Le seul composant qu'on retient pour l'inducteur est une résistant 'r', d'où la 1ière relation : la tension appliquée à l'inducteur 'v' s'équilibre avec le courant 'i' qui le parcourt comme indiqué.

Pour l'induit, il y a une résistant 'R' et aussi une force électromotrice d'expression 'k i Omega' (c'est le 'b S Omega' du cadre tournant, 'b S' dépendant linéairement de 'i' via un coefficient 'k'). D'où la deuxième relation.

Et finalement l'expression du couple électromagnétique du cadre s'écrit alors comme pour la troisième relation.

Ces équations sont suffisantes pour rendre compte du fonctionnement d'une machine à courant continue. Comme ce sera vu en TD.

Planche 11 : De la planche 7 à 10, on s'est occupé de la commutation comme méthode pour transformer le cadre tournant en une véritable machine électrique.

Mais il y a aussi la possibilité de créer une induction magnétique tournante. C'est à dire que 'b' reste uniforme en amplitude mais que sa direction change dans le temps.

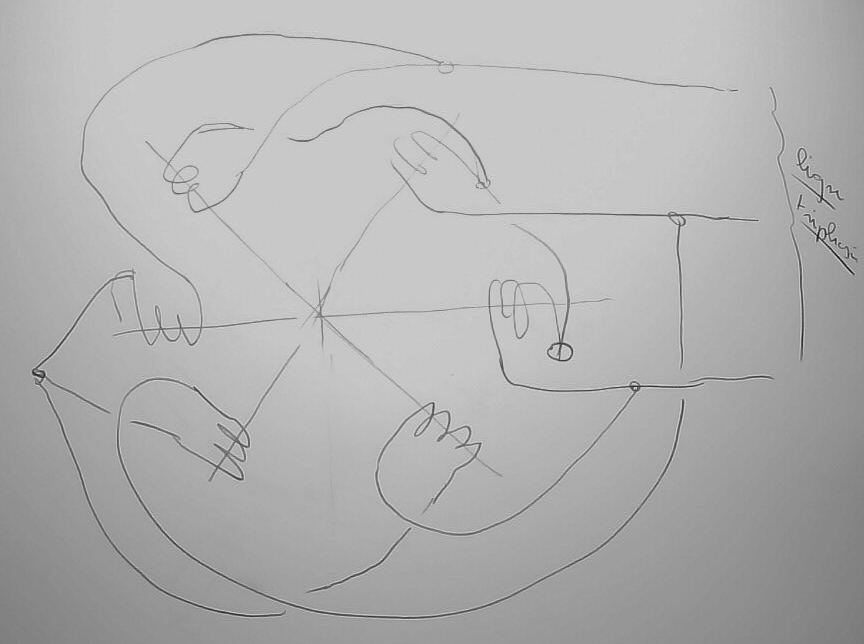
Pour cela, si on dispose trois enroulements comme sur la figure de gauche (et sans s'occuper de la carcasse sur laquelle ils sont bobinés) ; que ces trois enroulements sont alimentés par du triphasé ; alors l'induction magnétique dans la région intérieure est à peu près uniforme et sa direction dépend sinusoïdalement du temps. C'est ce qu'on appelle le champ tournant.

La fonction de la carcasse (ferro)magnétique est de canaliser ce champ bien mieux que ne le fait l'air.

La figure de droite représente une variante pour produire un champ tournant. Là les conducteurs de chaque phase passent dans des encoches d'une carcasse magnétique et il peut y avoir les conducteurs de deux phases différentes dans une même encoche.

La description de la façon dont on peut organiser ces passages de conducteurs pour obtenir un champ tournant relève d'un cours qui s'intéresse à la construction des machines électriques ; c'est hors sujet ici.

Toutefois, la question de la polarité des machines électriques n'est pas elle hors sujet.

Pour la comprendre on peut revenir à des enroulements comme ceux de la figure de gauche et examiner les courants à l'instant 't=0'. Les trois enroulements son identiques à 3 aimants de pôles : N-S ; S/2-N/2 ; S/2-N/2 comme sur la figure

On convient que si N dénote une valeur d'intensité de pôle, N/2 dénote la valeur moitié, la valeur d'intensité de pôle étant proportionnelle au courant dans l'enroulement.

Cet arrangement d'aimant correspond à une induction magnétique dirigée selon la double flèche. C'est ce qu'on appelle un polarité à 1 paire de pôles (les deux demi-pôles 1/2 étant vus comme un seul).

Maintenant, examinons un cas qui comporte plus d'enroulements.

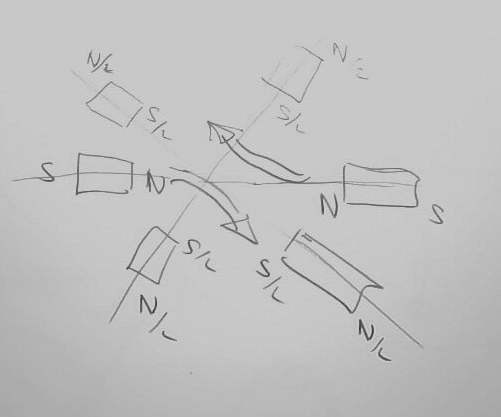
Il y a 6 enroulements qui sont connectés (en étoile) à une ligne triphasée.

En terme d'aimants équivalent cela correspond à

L'induction magnétique n'est pas uniforme. Et si on essaie de dessiner des chemins allant des pôles nords vers les pôles sud, on arrive aux deux flêches du dessin. Comme il y a deux flêches on dit que c'est une polarité de 2 paires de pôles.

Cette induction magnétique non uniforme qui correspond à deux paires de pôle n'agirait pas sur un cadre simple, mais si on fabriquait un cadre qui aurait aussi une structure à deux paires de pôles, alors il y aurait une action.

On peut ainsi fabriquer des inductions magnétiques de polarité quelconque. Mais quel est l'intérêt

On le trouve dans la dynamique. Pour expliquer la polarité on a examiné la situation à un instant donné. Mais comme les courants sont sinusoïdaux celle-ci change au cours du temps : un pôle qui était Nord devient Sud et vice-versa. C'est cela fait tourner l'induction magnétique (change sa direction).

Dans le cas d'une paire de pôle l'induction magnétique fait un tour complet pendant une période électrique.

Mais dans le cas de deux paires de pôles elle ne fait qu'un demi-tour pendant cette période. Du coup à fréquence électrique donnée on trouve que la fréquence mécanique est sa moitié.

Comme la fréquence électrique est donnée (50 Hz), la connaissance de la polarité permet de connaître la fréquence mécaniques (le nombre de tours par minute des moteurs). Ceci sera examiné dans l'exercice 2.

Planche 12 : Ce qui précède permet d'obtenir les équations de la machine synchrone. Et notamment celles de l'alternateur.

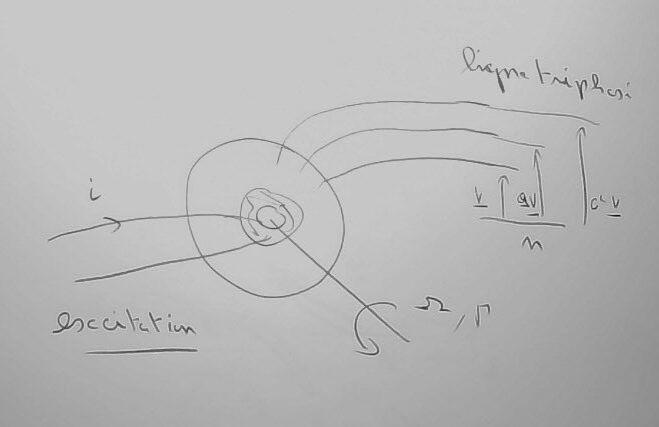
On doit voir cet alternateur comme

une machine qui est alimentée en courant au rotor (via des bagues) par un courant 'i' (il y a une force électromotrice continue qui force ce courant) ; ce rotor est entraîné en rotation à la vitesse 'Omega' (par une turbine) ; et en sortie il y a trois conducteurs de phase qui forment une ligne triphasées (ils sont connectés en étoile par exemple de façon interne).

La question qui se pose est alors celle de la tension 'V' en sortie de l'alternateur. Ce qui précède permet d'affirmer qu'elle a la forme indiquée ('I' étant le courant triphasé dans la ligne).

Planche 13 : Pour conclure, on pourrait dire un mot de l'approche synthétique qui pourrait être menée dans l'électromécanique des machines électriques de nature synchrone.

Mais je doute que le temps imparti permette de faire plus que d'indiquer que cette approche existe. Et même qu'elle est dans la continuité historique de la façon dont les modèles explicatifs de l'électromagnétisme ont été formés.