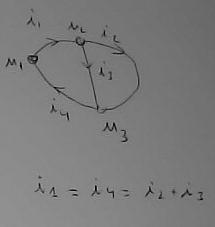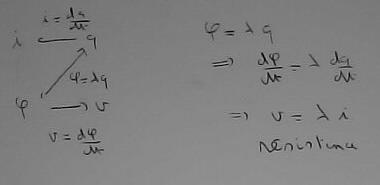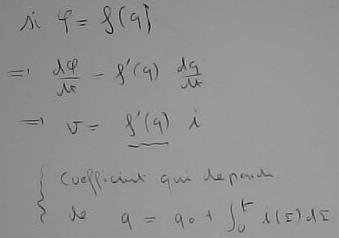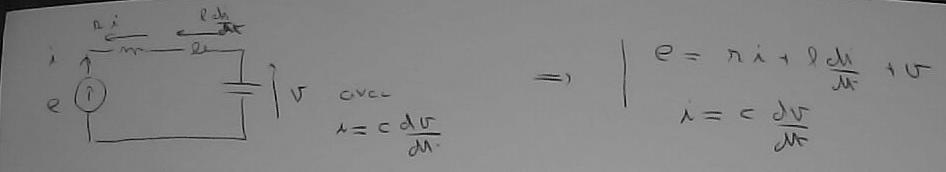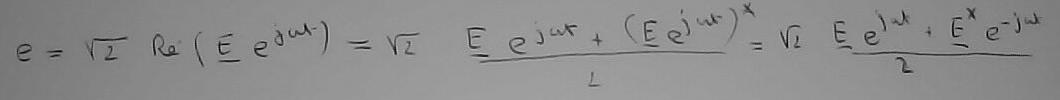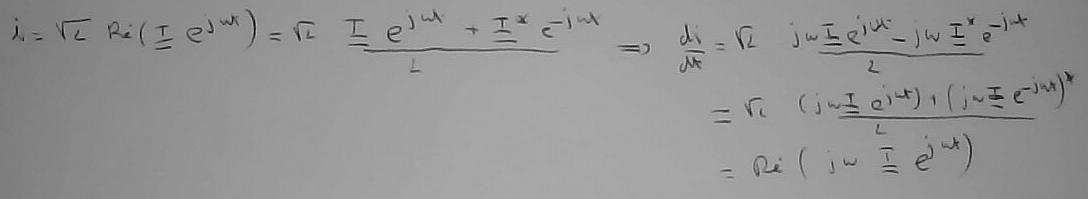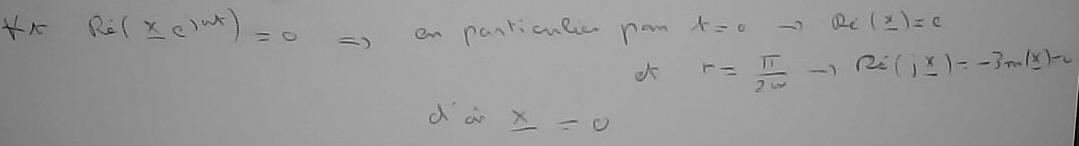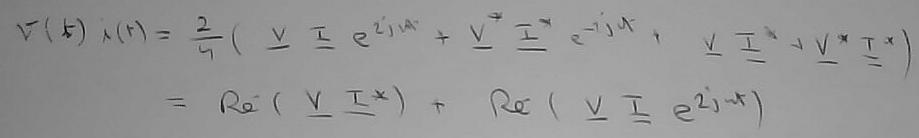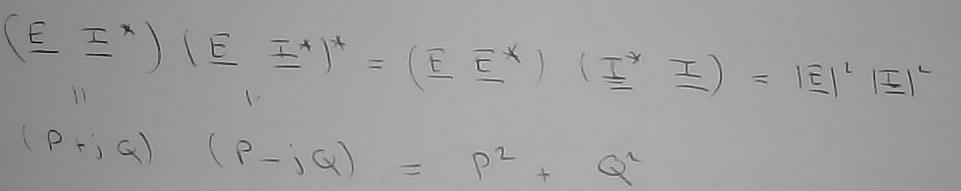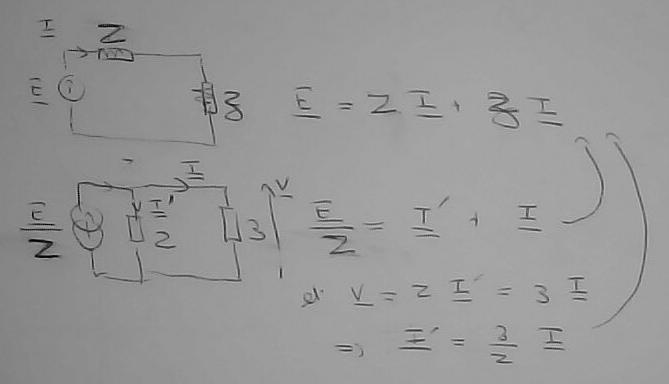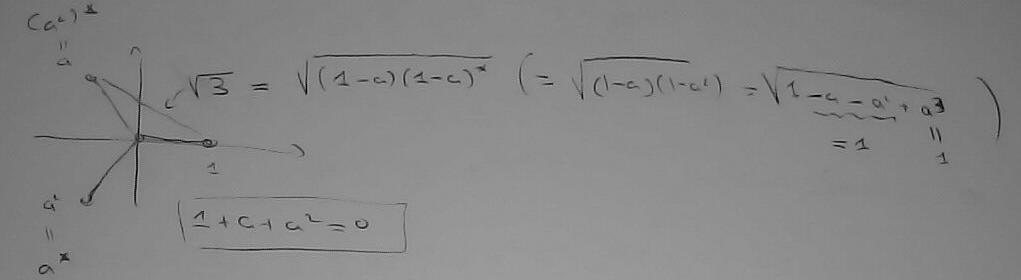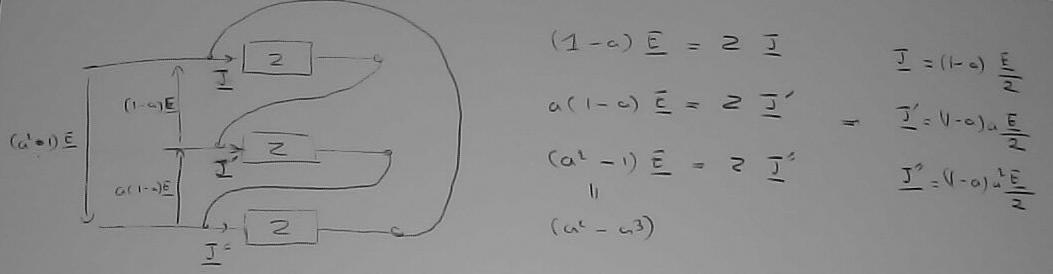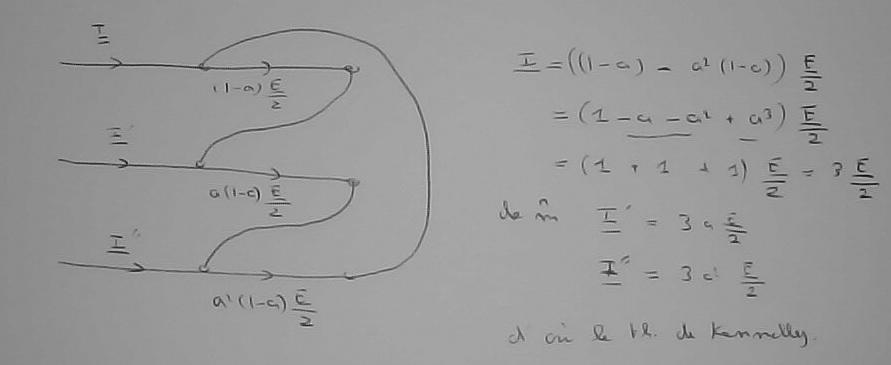Planche 1 : Cet enseignement a pour objectif d'introduire les notions et le vocabulaire du corps de disciplines qu'on appelle le Génie Électrique.

Dans des conditions normales, il est composé de 5 leçons : Circuits électriques mono et tri-phasé ; Production et transport de l'électricité ; Transformation de l'énergie électrique ; Machine asynchrone ; Conversion électromécanique. D'une séance de Travaux pratiques où nous vous présentons les objets réels dont les leçons ne peuvent que fournir les représentations en terme de modèles mathématiques. Et d'une séance d'application où les éléments de la leçon sur le transport de l'énergie électrique sont utilisés pour traiter d'un cas concret.

Cette année, la séance de travaux pratiques ne pourra pas avoir lieu. Nous n'avons pas encore décidé par quoi elle sera remplacée, probablement par une séance d'exercices.

L'équipe d'enseignants est composée de Stéphane Dufour et de moi-même, Gérard Vinsard. Nous alternerons la charge d'enseignement dans les leçons.

C'est un peu une gageure que de vouloir faire tenir en aussi peu de temps un programme qui en demanderait bien plus. Mais il s'agit essentiellement de faire en sorte que ceux et celles qui suivent l'enseignement acquièrent suffisamment de connaissance dans la matière pour pouvoir eux-même l'approfondir au cas où ils exercent leur activité dans un contexte où elle leur soit nécessaire.

Le test final qui aurait eu lieu sous forme d'un examen de 2 ou 3 heures en classe sera remplacé par cet examen que chacun devra faire chez lui sur feuilles libres qu'il devra scanner et envoyer à une adresse de dépôt (celle-ci par exemple ou ailleurs, nous la préciserons au moment venu). Le temps imparti à l'examen sera par exemple de 4h : à l'instant t (cet instant sera précisé) l'épreuve sera déposée et visible et à l'instant t+4h il faudra que toutes les copies soient déposées.

Bon, je pense avoir dit tout ce qui devait l'être. Sinon il est possible de demander des précisions dans le salon

Planche 2 : Les objectifs de cette première leçon sont ceux qui sont indiqués.

La seule nouveauté par rapport à ce qui est déjà connu est a priori le régime triphasé, mais il ne nous a pas paru inutile de faire quelques rappels sur le monophasé.

Entrons tout de suite dans le détail !

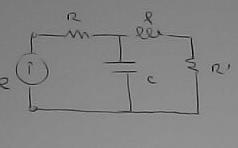
Planche 3 : Un circuit électrique est un schéma représentant des éléments reliés entre eux par des fils électrique comme sur cette photographie.

Ce schéma ressemble à quelque chose comme le dessin ci-dessous.

on dessine les éléments du circuit et on les relie par des traits.

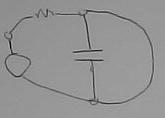
Certains de ces traits sont superflux. Si on se limite à la règle que chacun des éléments est relié aux autres par seulement deux fils et qu'on considère que les fils n'ont que la fonction de relier les éléments, il serait préférable de faire le dessin comme

Et si on va encore plus loin en ne considérant plus les éléments mais seulement la façon dont ils sont reliés entre eux on obtient

C'est très exactement un graphe : il y a des nœuds (les points jonctions entre les éléments) et les arêtes (les lignes imaginaires qui traversent les éléments) et c'est tout. On a réduit le circuit électrique à sa structure topologique (c'est un peu prétentieux mais ça se dit).

Les nœuds sont affectés d'une valeur, ici u1, u2, u3 ; ce sont les potentiels électriques. Les arêtes sont affectées d'une orientation (qui peut être prise au hasard) et d'une valeur qui est cohérente avec l'orientation ; ce sont les courants électriques, ici i1, i2, i3 ,i4.

Les courants électriques ne peuvent avoir des valeurs quelconques, elle doivent respecter la loi aux nœuds (des lois de Kirchoff).

Cette représentation de la structure du circuit électrique comme graphe peut apparaître comme un peu superfétatoire pour des circuits simples mais elle devient tout à fait nécessaire lorsque le circuit se complexifie.

Planche 4 : On continue la description du graphe du circuit.

Il y a la notion de courants incidents qui doit être claire.

Il y a aussi l'introduction des différences de potentiels : elles permettent de passer de grandeurs liées aux nœuds (les potentiel) à des grandeurs liées aux arêtes (les différences de potentiel ou tension).

Planche 5 : Le texte de la planche se suffit à lui-même.

Planche 6 : Là on réintroduit les éléments qui avaient été évacués pour ne garder que la structure de graphe.

Ces éléments sont appelé les composants. Et parmi ceux d'entre eux qu'on qualifie de passif il y a les résistance, autoinductance et condensateur.

Comme la structure de graphe a fait apparaître les courants et les tensions sur les arêtes qui étaient une schématisation des composants, ces composants se présentent mathématiquement comme une relation entre tension et courant.

On notera que ces 3 composants épuisent les possibilités de relation linéaire entre les tension, courant et leurs dérivées temporelles : toute relation de ce type correspond à un agencement de ces composants.

L'expression de la relation de l'autoinductance fait apparaître une grandeur intermédiaire qui est le flux magnétique : on n'écrit pas 'v = l di/dt' mais 'v = d phi /dt avec phi = l i'. On pourra certainement bien écrire 'v = l di/dt' mais il ne faut pas alors oublier que 'phi=l i' est une grandeur d'égale dignité à 'v' ou 'i'.

Et le même commentaire peut être fait pour le condensateur avec 'q', la charge électrique, comme grandeur intermédiaire.

Planche 7 : Pour bien comprendre les relations entre grandeurs tension (électrique), courant (électrique), flux (magnétique) et charge (électrique), on peut examiner ce qui s'appelle le diagramme de Chua.

Dans le dessin toutes les relations sont portées mais dans un composant elles ne sont pas toutes présentes simultanément, c'est plutôt comme sur le dessin ci-dessous

Les seules flèches utiles sont celles qui relient 'v' à 'i' ; pour la résistance, il y a bien 'phi' et 'q' mais ils ne sont pas utilisés ; pour l'autoinductance 'q' ne l'est ; pour le condensateur 'phi' ne l'est pas.

Ce schéma a une portée heuristique : on (Chua) s'est demandé pourquoi il n'y avait pas un composant pour lequel il y aurait une liaison entre 'q' et 'phi' ?

Et il a examiné ce que ça donnerait, soit

Mainfestement c'est une résistance, donc rien de nouveau !

Par contre, si la relation entre 'phi' et 'q' était non-linéaire

le composant ressemble à une résistance dont la valeur dépend de l'histoire du courant qui l'a parcouru, là c'est nouveau.

Et c'est le début de l'histoire du memristor

Nous ne nous occuperons pas du memristor. Cette planche avait pour unique objectif de montrer que, tout étant dans tout, rien n'est petit :) et plus sérieusement d'insister sur la structure des équations de circuit.

Planche 8 : Après les composants passifs, voici les composants actifs.

Ce sont les générateurs de tension et de courant. On remarquera que leur introduction correspond à passer d'une relation linéaire entre 'v', 'i', 'q' ,'phi' à une relation affine entre ces grandeurs.

Pour le générateur de tension, la relation 'v = -e' mérite cependant une explication.

Quel que soit le composant les sens des flèches de tension et de courant sont opposées l'un à l'autre : c'est ce qui s'appelle la convention récepteur. Pour la résistance ça permet d'écrire que 'v i = r i^2' et comme 'r i^2' est la puissance dissipée dans la résistance, la convention récepteur est telle que cette puissance, qui est donc injectée à la résistance, soit comptée positivement, ce qui est l'usage.

Pour le générateur de tension écrit avec la convention récepteur, la puissance est '- e i', si ce générateur était connecté à une résistance, on aurait 'i = e/r' et cette puissance serait '-e^2 /r' soit un quantité négative qui représente la puissance extraite du générateur pour être injectée à la résistance.

On peut aussi changer de convention pour les composants actifs en utilsant pour eux (et eux seuls) la convention émettrice, mais c'est un peu... disons donner le bâton pour se faire battre que d'entretenir les deux conventions dans un même circuit.

Planche 9 : Tous les éléments de modélisation sont en place et il s'agit maintenant de les exploiter.

Le circuit le plus simple est le circuit 'rlc' (i.e. 'r', 'l', 'c' en série -- et on est d'accord que la signification des locutions 'en série' et 'en parallèle' est suffisamment claire pour qu'il ne soit pas nécessaire de la rappeler) alimenté par une source de tension 'e'.

Les deux équations de la première ligne sont obtenues par la loi aux mailles.

Si 'e' est sinusoïdal, on lui donne une expression à base de complexes

'*' signifiant conjugaison.

La solution des équations différentielles ordinaires (EDO) comporte une partie transitoire et une partie de régime sinusoïdal établi. On ne s'intéresse qu'au régime sinusoïdal établi où le courant 'i' et la tension 'v sont de la forme indiquée.

La dérivée du courant s'écrit comme

Idem pour la tension, et il suffit de remplacer les EDO par les expressions complexes. Comme

il vient qu'on obtient les expressions algébriques indiquées portant sur les amplitudes complexes en lieu et place des EDOs.

Planche 10 : Jouer avec les lois de Kirchoff et les relations entre courant et tension des composants d'un circuit serait une activité futile si ça ne servait pas à chauffer ou faire bouger.

Il y a donc une énergie électromagnétique (on l'appelle ainsi plutôt qu'énergie électrique) et cette énergie électromagnétique peut se convertir en énergie cinétique (et réciproquement). Et cela se fait au prix d'une perte sous forme d'énergie thermique (en appelant ainsi l'énergie cinétique d'agitation des composants de la matière sous ceux de leurs modes qui correspondent à la chaleur).

Comme on s'intéresse essentiellement aux échanges d'énergie par unité de temps, c'est cette grandeur, soit la puissance, qui est considérée.

Une remarque : la description précédente évacue le rayonnement électromagnétique. Celui-ci a des effets négligeables aux fréquences qui sont effectivement utilisée dans la pratique, d'où l'oubli. On peut dire que l'électrotechnique est de l'électromagnétisme sans lumières, voire terne :)

Ce babillage fait, la question pratique est d'exprimer de façon générale la puissance entrante dans un ensemble de composants élémentaire qu'on peut appeler dipole). En convention récepteur c'est le produit 'v i'.

Si donc on examine le dipole formé des composants 'r', 'l' et c', On peut calculer le produit 'v i' en régime sinusoïdale établi comme

Comme la tension à ses bornes est 'v = e', on obtient le résultat indiqué. La puissance fluctuante est de moyenne temporelle nulle, elle ne contribue pas globalement à de l'injection de puissance et donc on ne s'en occupe pas (en 1ière approximation).

À partir du moment où s'introduit une quantité (complexe) 'E I*' dont la partie réelle est quelque chose qui a un sens physique (la puissance injectée), on peut se demander si la partie imaginaire de 'E I*' n'a pas elle aussi un sens physique.

Il y a deux écoles sur la question : la première estime que oui et la seconde que non. Mais l'opinion qu'on peut en avoir n'est pas très importante dès lors qu'on s'accorde sur l'idée qu'a minima cette partie imaginaire (appelée la puissance réactive) est un intermédiaire de calcul très utile comme on le verra sur l'exercice No1.

Ces puissances apparente, active et réactive sont liées par la dernière expression de la planche qui s'obtient par un petit calcul

Planche 11 : L'expression de la puissance apparente commplexe pour le circuit 'rlc' est alors obtenue en utilisant les relations algébriques précédentes.

On note que le seul composant qui correspond à une puissance active non nulle est la résistance.

Planche 12 : la présentation précédente était une approche analytique du passage des EDOs aux équations algébriques sur les amplitudes complexes du régime établi.

On ne la reproduit jamais en électrotechnique, on utilise plutôt une approche synthétique oùon ne considère que les amplitudes complexe ; les autoinductances, capacité et résistance devenant des composants dont la relation entre tension et courant est 'V = i l omega I', 'V = I / (j c omega)', 'V = r I'

La locution de 'circuit monophasé' correspond à cette synthèse.

Planche 13 : Comme expliqué, dans le dessin des circuits, on porte les valeurs d'impédances plutôt que les coefficients comme labels des composants.

Et on utilise les nom des amplitudes complexes (majuscule souligné) plutôt que les nom des fonction du temps pour les courants et tensions.

La linéarité entre tension et courant obtenue permet de se livrer à des transformations sur le dessin du circuit qui correspondent à des manipulations algébriques des relations.

Par exemple, ce qu'on appelle les forme de Norton et Thévenin d'un même circuit correspond à

ça sert à remplacer une source de courant par une source de tension équivalente (et réciproquement) dans un problème de circuit. Le 'z' du dessin précédent est l'impédance équivalente du circuit passif représenté par le cercle dans le dessin de la figure.

Il fut une époque où il était très important de savoir transformer les circuits sur leurs dessins parce qu'on ne disposait pas de moyens automatiques de résolution d'équation algébriques symboliques.

De nos jours on dispose de tels moyens. Et c'est donc moins important. Ce qui ne veut pas dire qu'il ne soit pas utile de savoir « lire » un dessin de circuit...

Planche 14 : L'essentiel de ce qui était à dire sur les circuits monophasé est dit.

Il est donc possible de passer aux circuits triphasé équilibrés.

On considère un circuit monophasé comme celui de la planche avec des sources de tension ont la forme indiquée où 'a' est tel que

Ce circuit présente suffisamment de symétries pour que le calcul de ses grandeurs se ramène à celui d'un circuit monophasé plus simple.

Lorsque des situations de ce genre se présentent on dit que le circuit est triphasé équilibré.

Planche 15 : Montrons cela !

On décide que le potentiel du nœud de gauche est 0 et celui du nœude de droite 'V'. (on aurait prendre 'W' et 'Q' mais comme c'est 'Q-W' qui serait apparu, ce choix est licite.

La première ligne ne comporte aucune hypothèse sur 'Ia', 'Ib', 'Ic'

On fait la somme des trois relations de la ligne, la loi aux nœuds impose que 'Ia+Ib+Ic=0', d'où 'Ea+Eb+Ec = 3 V' mais 'Ea+Eb+Ec E (1 + a + a^2) =0' et donc 'V=0'.

Il reste alors les relations linéaires de la dernière ligne qui permettent d'écrire les courants comme indiqué sur le dessin.

Planche 16 : Suite

Et on constate que chacun des trois circuits est équivalent à l'un d'entre eux qu'on considère comme générique et qu'on appelle le circuit monophasé équivalent.

Planche 17 : Reste à examiner les puissances.

Pour cela on revient à la considération des trois circuits vus comme un seul circuit monophasé (et donc pas le circuit monophasé équivalent).

Les puissances apparentes issues de chacun des sources s'ajoutent (prende des indices 1,2,3 plutôt que a,b,c). Et en écrivant : 'En = a^(n-1) E', 'In = a^(n-1) I' pour 'n=1,2,3', cette somme est 'E I* + (a E) (a I)* + (a* E) (a* I)* = E I* + E I* a a* + E I* a* a = 3 E I*'.

Donc, pour les circuits triphasé, on considère le circuit monophasé équivalent pour calculer les amplitudes complexes et lorsqu'il s'agit de calculer la puissance apparente complexe (qui contient les puissance active et réactive) on multiplie par 3 la puissance apparente complexe obtenue pour ce circuit monophasé équivalent.

Un point important est que la puissance fluctuante d'un circuit triphasé équilibré est nulle. La puissance fluctuante de chacun des circuits qui le composent n'est elle pas nulle mais leur somme est nulle.

Lorsqu'on examinera les production et consommation d'électricité avec des alternateur et moteur, on verra que c'est une propriété dont l'importance pratique est considérable.

Planche 18 à 20 : Le contenu des planches doit être juste, mais je ne comprends plus bien leur ordonnancement, aussi je propose que vous commenciez à regarder ce commentaire avant de les regarder.

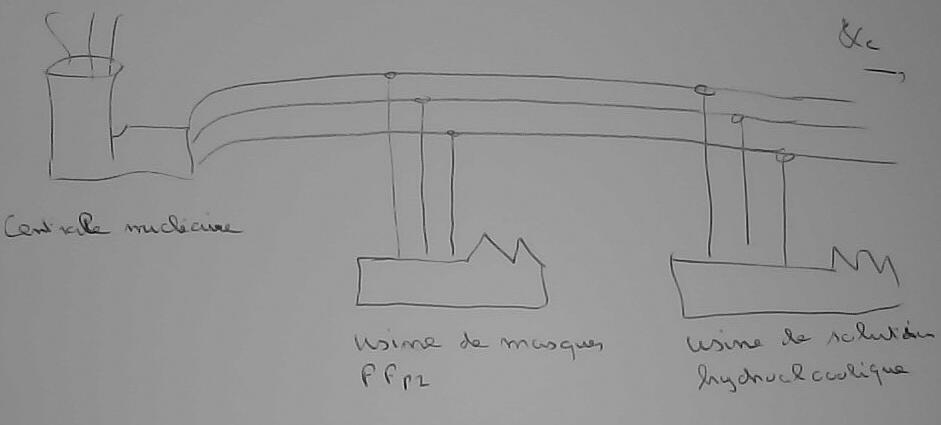
considérons la situation réelle des lignes triphasée. Il y a trois fils (avec peut-être un fil supplémentaire, M Dufour expliquera mieux comment c'est organisé) qui partent... mais ce dessin est plus explicatif

On fait l'hypothèse que les tensions 'E', 'a E', 'a^2 E' ne varient pas le long de chacun des trois fils horizontaux. Et donc la tension source à l'entrée de chacune des usines est de cette forme'E', 'a E', 'a^2 E'.

Donc, une charge triphasée (une usine) doit être connectée aux trois câbles (c'est un terme meilleur que fil) d'amenée. Mais comment le faire ?

Il y a les deux possibilités indiquées sur le dessin : en étoile et en triangle.

La connexion en étoile est conforme à ce qui a été présenté : les courants dans les trois impédances 'Z' sont : 'E/Z', 'a E/Z' et 'a^2 E/Z'.

La connexion en triangle, par contre, demande à être examinée. Pour cela on commence par caluler les « J », « J' », « J'' » du dessin

Plutôt que d'utiliser les tensions entre chaque câble (qu'on appelle phase) et le neutre (le portentiel du centre de l'étoile lorsque les phases sont reliées en étoile (via une impédance) on utilise les tensions entre phase (M Dufour fournira les éléments de langage d'usage), d'où les tension indiquées.

On arrive alors à voir que ces courants « J », « J' », « J'' » sont en raison de 'a' ; on dit qu'ils forment un système triphasé.

Puis on calcule les courants « I », « I' », « I'' » du dessin

et on voit qu'ils forment un système triphasé.

C'est exactement celui qu'on aurait obtenu en connectant des impédances 'Z/3' en étoile. Et c'est ce qu'on appelle le théorème de Kennelly.

D'une façon générale, on peut toujours procéder ainsi pour transformer les connexions en triangles en connexions en étoiles équivalentes, mais, avec un peu d'habitude, on sait qu'on retombera toujours sur des résultats similaires qu'on peut facilement deviner en ne faisant que partiellement les calculs.

Planche 21 : Les bobines couplées

Tout semble indiqué sur la planche...

Planche 22 : Les bobine triphasés équilibrées et couplées

Idem. On reviendra là dessus.

Exercices : :

Faites déjà le No1 du polycopié. C'est un exercice classique qu'il convient de bien savoir faire.

Et continuez avec les exercices suivants.

J'ai préparé les corrections mais je ne les mettrai en ligne (sur ce salon et sous forme d'images) que par petits morceaux et à la demande.