Planche 1 : J'ai en charge d'assurer deux cours magistraux dans le cadre du cours de CAO.

Ces cours ont pour objectif de rappeler les éléments d'électromagnétisme de base qu'utilisent les électrotechniciens.

Le premier de ces cours porte sur la magnétostatique et rappelle les modèles qui permettent de décrire : les aimants permanents, les courants électriques et l'aimantation induite.

Planche 2 : Tout d'abord, un petit détour. Qu'est-ce-que la gravitation (non relativiste) ?

Il y a un espace absolu (celui de Newton) et dans cet espace sont disposées des masses supposées réparties avec la densité rho.

On calcule la fonction Phi (appelée potentiel newtonien), solution du problème indiquée. Et on définit le champ de gravitation G comme -grad(Phi).

Ce champ de gravitation sert à calculer la force globale qui s'exerce sur un domaine D quelconque, ainsi que le couple Gamma. Si donc les masses dans ce domaine D étaient liées entre elles comme dans un solide indéformable qui occuperait la région de l'espace D, on disposerait des éléments permettant de calculer son mouvement.

Mais c'est au prix du recalcul de G chaque fois que les masses se sont effectivement déplacées les unes par rapport aux autres.

Quel rapport avec la magnétostatique ? Et bien, c'est écrit dans la planche.

Planche 3 : Il est intéressant de voir le passage de la gravitation à la magnétostatique comme un simple changement des détails de calcul dans une même structure.

Pour la gravitation il y a la donnée des masses et on en déduit in fine une force qui s'exerce sur ces masses

Pour la magnétostatique il va falloir préciser par quoi on remplace les masses : ce sera par des aimantations et des courants électriques.

Par contre une complication va s'introduire qui n'existe pas dans la gravitation, c'est celle de l'aimantation induite dans les milieux magnétiques (enfin peut-être... il ne semble pas exister pas de matériaux dont la masse change sous l'effet du champ de gravitation, mais sait-on jamais. Avec les méta-matériaux ?). Il nous faudra expliquer cela.

Comme le cours est d'un volume limité, on ne parlera pas des énergie et coénergie magnétiques qui sont pourtant les concepts essentiels donnant accès à tout le pandémonium des notions propres de l'électromagnétisme.

Mais à chaque jour suffit sa peine :)

Planche 4 : Commençons par la description des aimants permanents. Et déjà l'aimant immobile (qui est en peu le pendant de l'eau sèche de Feynman).

Prenons de ces petits aimants (fabriqués et aimantés en chine, comme vous-savez-quoi) qu'on peut acheter comme jouets

chacun d'entre eux (il y en a 13) possède une aimantation uniforme dans son volume : celle-ci est une quantité vectorielle m_n contante et l'aimantation d'un seul aimant est (presque cf ce qu'on dit sur l'unité infra) ce vecteur dans son volume. Si on étend l'aimantation à tout l'espace, cette aimantation est le vecteur m_n dans l'aimant et 0 ailleurs.

Pour représenter les 13 aimants, on a besoin d'introduire une aimantation globale. Et une possibilité est de la définir comme indiqué dans la planche. Où Dn est la région de l'espace occupée par l'aimant n.

Les régions (on dit plutôt domaine en français) peuvent varier dans l'espace. Par exemple on peut disposer les aimants comme

Du point de vue des unités la densité d'aimantation est en A/m et ce qu'on appelle l'aimantation est le produit de cette densité par le volume de l'aimant, elle est donc en A m^2.

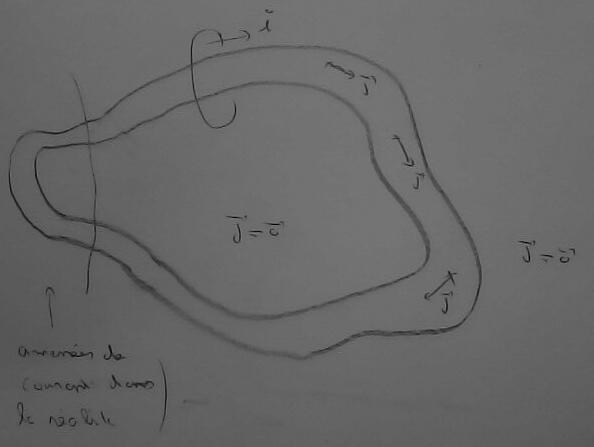
Planche 5 : Il n'y a pas que les aimants dans le monde (sublunaire). Il y a aussi les courants électriques.

On représente un courant électrique par sa densité de courant j (en A/m^2). Cette densité est un champ de vecteur défini dans tout l'espace et nul partout où soit il n'y a pas de conducteurs d'électricité soit ceux-ci ne sont pas alimentés.

Une bonne image du courant électrique est celle de tuyaux d'eau fermés sur eux même où d'invisibles démons (de Maxwell) pousseraient les particules d'eau pour qu'elle circulent dans les tuyaux. Le courant électrique serait alors le débit massique d'eau (kg/s) et la densité de courant électrique la densité de quantité de mouvement des particules d'eau (kg/m^3 x m/s) qu'il faut multiplier par (ou plutôt intégrer normalement sur) la surface (m^2) de la section du tuyau pour retrouver le débit. À ceci près que plutôt que de mettre une masse en kg, on change sa nature en charge électrique en C (l'ampère est le Coulomb par seconde).

Avec cette image, et aussi la connaissance empirique que pour l'hydraulique ordinaire (hors pompes bélier) l'eau peut être considérée comme incompressible, on arrive à l'idée que la densité de courant est à divergence nulle dans tout l'espace.

Toujours avec cette image, on peut séparer le support du courant d'eau de son débit et faire de même pour le courant électrique de manière à l'écrire comme indiqué.

Le dessin ci-dessous précise les choses

Le courant électrique est amené par des amenées de courants mais, pour le calcul, on représente le domaine du courant comme fermé sur lui-même (en forme de tore) : pour cela on considère que les amenées de courants sont fermées sur elles-même et que le courant qui vient des portions de domaine où circule effectivement du courant (la partie des amenées qui est éliminée par l'approximation) ne contribue en rien à la production de champ et induction magnétique

Intermède 1 : Mine de rien, on est arrivé à décrire ce qui remplace la masse dans le passage du problème de gravitation au problème de magnétostatique.

Il reste maintenant à décrire ce qui va remplacer le champ de gravitation.

Planche 6 : Commençons par les aimants permanents.

Ce qui est écrit dans la planche demande de changer de point de vue. Pour introduire les densités d'aimantation et de courant on s'est contenté de donner des propriétés (guère différentes de la masse) à des matières appelée aimant et conducteur de l'électricité. Maintenant on plonge dans quelque chose de plus abstrait, du moins moins tangible.

On (en fait Helmholtz) étudie mathématiquement les propriétés du champ de vecteurs qu'on a appelé la densité d'aimantation et on trouve que ce champ de vecteurs se décompose en parties solénoïdale (à divergence nulle) et irrotationelle (à rotationnel nul) : (au facteur mu0 et au signe - devant h près) l'induction magnétique b et le champ magnétique h.

Ça pourrait ne servir à rien. Mais il se trouve que ça va servir à identifier ce qui jouera le rôle du champ gravitationnel pour le calcul effectif des forces et couples que des aimants exercent les uns sur les autres.

Planche 7 : La décomposition d'Helmholtz permet de trouver deux problèmes (i.e. deux systèmes d'équations) dont b et h sont solutions indépendamment l'un de l'autre.

Chacun de ces problèmes a pour source (i.e. le terme connu dans le problème tel que s'il était nul alors le champ inconnu serait nul aussi) une quantité dérivée de m : le rotationnel de m pour b et la divergence de m pour h.

On voir alors que chacun des problèmes a la même structure que celui qui fournit le potentiel newtonnien dans le problème de la gravitation du détour de départ.

Intermède 2 : Il est nécessaire d'examiner ce que sont rot(m) et div(m).

La difficulté vient de ce que ce ne sont pas des champs de vecteurs réguliers et qu'il doivent plutôt être représentés par des distributions.

Exactement comme pour les dérivées de fonctions de R dans R discontinues dans le cours sur les distributions de 1A.

Le cours sur les EDP de 1ier semestre de cette année a repris ces notions en introduisant la dérivée faible des champs de scalaire. C'est la même chose pour les champs de vecteurs.

Comme tout cela n'est pas si facile, cette présentation contient une annexe (planches 25 à 33) rappelant les principales notions.

Planche 8 : Occupons nous de rot(m) qui s'appellera le courant ampérien du système d'aimants que représente m.

Pour l'examiner, on en fait le produit scalaire avec un champ de vecteur quelconque a et on intégre sur tout l'espace : ce serait le produit scalaire dans L2 si rot(m) était un élément de L2 (ce qu'il n'est pas).

Puis on intégre par partie ce qu'on a obtenu. Là c'est bien un produit scalaire d'élément de L2 (m est dans L2 et rot(a) également puisque a est indéfiniment différentiable sur toutes ses composantes).

Le terme int_{E3} rot(m) . a dV est donc un quantité bien définie quand a est connue. On a ainsi spécifié ce qu'était la distribution qui représente rot(m).

Et on peut y exprimer que m est constante par morceaux sur les domaines Dn.

Planche 9 : L'expression de int_{E3} rot(m) . a dV lorsque m est constante par morceaux peut être précisée.

Elle conduit aux produits scalaires des mn par un vecteur intégrale de surface sur les bords de Dn qui dépend de a et non plus de ses dérivées.

On a obtenu le résultat cherché : rot(m) s'exprime sous forme de distribution à partir des distributions de Dirac de surface sur les bords des Dn. Ce sont les courants ampériens des aimants.

Planche 10 : Il est possible de la même façon de spécifier div(m)

Mutatis mutandis, on obtient ce qui est appelé les masses magnétiques.

Planche 11 : rot(m) et div(m) étant spécifiés, on réécrit avec ces spécifications les problèmes de la planche 7

Et du fait de la linéarité des problèmes, on peut décomposer b et h comme somme des bn et hn. bn et hn qui sont les induction et champ magnétiques de l'aimant n seul et sont solution des problèmes indiqués en bas de la planche.

Planche 12 : Les deux façons de considérer les aimants.

Tout est dit dans la planche.

Planche 13 : Occupons nous maintenant des courants électriques.

On affirme qu'à une densité de courant j donnée on peut associer des induction et champ magnétiques comme indiqué.

A priori pas de rapport entre ces nouveaux induction et champ et ceux qui avaient été défini pour les aimants.

Mais Oersted a montré (expérimentalement) qu'il étaient indiscernable quand à leurs effets (dont on n'a pas encore parlé)

Si on connait ces induction et champ dans une portion de l'espace extérieure à la source (m ou j) qui les produit, on ne peut savoir si c'est un courant électrique ou un aimant qui les a produit.

Ceci étant dit, on procède comme pour les aimants pour obtenir par superposition les champ et induction d'un courant seul.

Planche 14 : Puisque on ne sépare pas les courants électriques et les éléments, on peut faire la synthèse indiquée dans le transparent.

Cette synthèse n'aurait pas été aussi directe avec la représentation coulombienne des aimant. C'est sans doute la raison pour laquelle les électrotechniciens privilégient leur représentation ampérienne.

Il y a un exercice à faire en footnote. Je vous suggère d'y réfléchir (après le cours) avant de regarder la solution planche 34.

Planche 15 : les induction et champ magnétiques sont comme le champ de gravitation. Ils ne servent à rien tant qu'il ne sont pas utilisé pour calculer des forces.

La force due à ces induction et champ se représente déjà sous la forme de la densité de force de Laplace. Celle-ci s'exerce sur les supports matériels à la fois des densités de courants électriques et des densités de courants ampériens des aimants.

Lorsqu'on décompose les densité en densités propre aux solides Dn qui en sont les support, on peut obtenir les force et couples globaux qui s'exercent sur ces solides.

Le fait que les intégrales portent sur E3 ne doit pas cacher que : pour les courants électriques jn est nulle en dehors de Dn (et donc l'intégrale ne porte effectivement que sur Dn) ; pour les aimants elle est nulle en dehors du vbord de Dn (et dont l'intégrale porte sur ce bord).

Intermède 3 : Voilà ! Ce qui était annoncé est réalisé.

Planche 16 : Cependant il reste les difficultés décrites brièvement dans la planche pour la mise en pratique des calculs effectifs.

Planche 17 : Abordons maintenant la question du magnétisme induit.

Ce n'est pas une question simple !

Mais elle peut être simplifiée (en première intance) avec l'approche phénoménologique décrite.

Sur le plan sémantique, on convient d'appeler 'domaine magnétique' le support des matériaux magnétiques pour lesquels la susceptibilité magnétique n'est pas nulle.

Planche 18 : L'introduction des domaines magnétique transforme le problème de la planche 14 en celui qui est indiqué ici.

Où, plutôt que la susceptibiité magnétique, on utilise la perméabilité magnétique.

Planche 19 : La présence des domaines magnétiques ajoute un terme à la densité de force de Laplace. Appelons le la pression magnétique.

La pression magnétique a comme support les bords des domaines magnétiques Dp.

Dans les moteurs électriques, il y a des courants (électrique et/ou les ampériens des aimants) et des carcasses en matériaux magnétiques. Le couple que les stator et rotor exercent mutuellement l'un sur l'autre a essentiellement pour support les carcasses magnétiques.

Sinon, d'ailleurs, il y aurait des difficultés mécaniques pour faire des moteurs électriques puisque ni le cuivre des conducteurs électrique ni les aimants ne sont particulièrement résistants. Contrairement aux carcasses magnétiques.

Ceci pour bien insister sur l'importance pratique de la pression magnétique !

Planche 20 : La pression magnétique permet de calculer les force et couple sur chacun des domaines magnétiques Dp comme indiqué.

Et sa considération permet également de déduire des effets qualitativement.

Planche 21 : La densité de force cumulée (Laplace et magnétique) peut s'écrire comme la divergence d'un tenseur T d'ordre 2 appelé le tenseur de Maxwell.

Il est intéressant de refaire les calculs qui sont tout à fait dans la ligne de ce qui a été vu en mécanique des milieux continus (notation en indices répété et tutti quanti).

Planche 22 : L'intérêt du tenseur de Maxwell, qu'on devrait plutôt appeler champ de tenseur de Maxwell, vient de ce que ce champ est régulier.

Sa divergence (la densité de forces) ne l'est pas (c'est une distribution), mais lui il l'est !

Du coup sa considération permet d'éviter des difficulté de calcul des force et couple électromagnétique.

Intermède 4 : Comment calculer effectivement l'induction magnétique !

Planche 23 : On peut introduire le potentiel vecteur magnétique.

Un résultat du à Poincaré affirme qu'un champ à divergence nulle dans tout l'espace est le rotationnel d'un autre champ qu'on appelle son potentiel vecteur.

Il suffit alors d'exprimer le problème de magnétostatique à partir du potentielvecteur magnétique a seul

Pour que a soit défini de façon unique on ajoute une condition (dite de jauge) pour qu'il le soit. Il y a plusieurs façons d'introduire une telle condition mais l'une d'entre elle, qui est trs utilisée en électrotechnique, consiste à choisir a parmi les champs solénoïdaux (à divergence nulle).

Et on obtient le problème elliptique indiqué qui se prête aux résolution par éléments finis (voir partie M Dufour).

Planche 24 : Pour finir, on peut introduire un sous-produit du résultat de calcul du potentiel magnétique qui est particulièrement intéressant en électrotechnique : le flux magnétique.

Le flux magnétique associé à un courant in de support un est le phin indiqué.

Ce flux est celui qui est relié aux courants p (p = ou différent de n) par les coefficients d'inductance.

Conclusion : Voilà ! Les éléments essentiels pour la modélisation de dispostifs électromécaniques sans induction électrique (ce n'est pas l'induction magnétique) sont présentés.

Les transparents qui suivent sont des annexes.

Il y a l'annexe mathématique qui fait le lien avec le cours d'EDP.

Et, après les solutions des deux exercices proposés, le calcul complet des champ et induction d'un aimant sphérique (juste pour mémoire).