 (Pratico-)pratique du calcul symbolique et numérique --
(Pratico-)pratique du calcul symbolique et numérique -- Séminaire, 20 mai 2012, 13h45 Lien Teams
Tout (v)oir / (c)acher Motivation Empilement Emacs Maxima Appariteur Calcul Différentiel Élémentaire Formule de Stokes Chaîne élastique En guise de conclusion
Il y a les phénomènes et leurs modèles.
En physique appliquée, les modèles sont donnés (légués par les grands anciens) et il s'agit de les paramétrer pour qu'ils décrivent au mieux le fonctionnement d'un dispositif (ou d'une classe de dispositifs) ; ce fonctionnement étant une réalisation des phénomènes.
Les modèles se présentent sous la forme de conditions mathématiques portant sur des variables, ces dernières étant : soit reliées à ce qu'on peut observer dans le fonctionnement du dispositif ; soit des intermédiaires à partir desquels on peut former d'autres variables du type précédent.
Très souvent les conditions mathématiques ne permettent pas directement de déterminer les valeurs des variables. Il faut procéder à une résolution. On parle alors d'équations à résoudre. Et cette résolution passe par un
On ne sait pas en général résoudre les équations, il faut donc les manipuler pour les mettre sous une forme où il devient possible de les approximer. Cette activité est encore un
Et finalement, après avoir obtenu les valeurs des variables, il est encore souvent nécessaire de pratiquer des
Pour fixer les idées, voici
Ce sont des
Un autre objectif de cette présentation est de montrer par l'exemple ce qu'on peut réaliser en terme de praxis du calcul en utilisant uniquement des outils libres.
Et cela fonctionne encore sous Windows 10 (au prix de l'installation d'Emacs, Maxima et FreeFem++ qui se portent bien via Cygwin). Sur MacOS, sans doute aussi puisque c'est un Unix déguisé, mais contrairement à Windows je n'ai pas porté mes outils dessus...
On cherche les conditions de stabilité de l'empilement d'une boule posée sur trois autres, comme ceci
Vidéo démonstrative : le petit cube jaune est un aimant qui maintient les boules en place. Lorsqu'il n'y est plus, les boules roulent et glissent !Ces conditions s'exprime avec la loi de Coulomb : d'une part entre deux boules et d'autre part entre le plan et les boules qui reposent dessus. Tous calculs faits on trouve


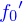 très petit, l'équilibre sera déterminé par la valeur de
très petit, l'équilibre sera déterminé par la valeur de 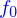 ; et inversement si le frottement entre les billes et le plan est négligeable c'est la valeur de
; et inversement si le frottement entre les billes et le plan est négligeable c'est la valeur de 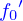 qui gouverne l'équilibre.
qui gouverne l'équilibre.
C'est intéressant, Mais la question est surtout celle de la manière dont on peut mener les calculs qui amènent à ces relations.
À l'ancienne, on ferait un dessin plus ou moins précis des 4 boules ; sur lequel on constaterait que la symétrie permet de ne retenir que les forces de réaction : d'une boule avec le plan et de cette boule avec la boule du dessus. Ces deux forces seraient nécessairement dans le même plan et donc on n'aurait que 4 composantes à calculer.
Mais la suite reste quand même un exercice de géométrie analytique sordide de ce genre.
Avec les moyens actuels de calcul symbolique, il est possible d'introduire toutes les forces sans prendre en compte la symétrie et d'en chercher leurs valeurs à l'équilibre.
Déjà la géométrie, si les trois boules reposant sur le plan sont numérotées 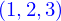 , que la boule du dessus est numérotée
, que la boule du dessus est numérotée 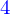 , que le plan est numéroté
, que le plan est numéroté 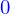 , les coordonnées des centres des boules sont
, les coordonnées des centres des boules sont
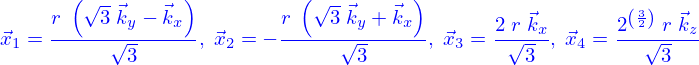
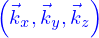 est une base cartésienne et
est une base cartésienne et  est le rayon des boules.
est le rayon des boules.
Ces expressions sont obtenus par un calcul dont le script est
addv(x)$Indicie([1,2,3,4],x)$ rcu:map(second,solve(z^3=1,z))$ Co2Vec(%z):=block([],realpart(%z)*kx+imagpart(%z)*ky)$ rcu:map(Co2Vec,rcu)$ Pos:[x1=d*rcu[1],x2=d*rcu[2],x3=d*rcu[3],x4=D*kz]$ Eq:xtav(ev([nrm(x1-x2)^2=4*r^2,nrm(x1-x4)^2=4*r^2],Pos))$ solve(Eq,[d,D])$ sol:solve(Eq,[d,D])[4]$ Pos:factor(ev(Pos,sol))@Sans entrer tout de suite dans les détails du script, on utilise le plan d'Argand pour trouver les coordonnées des boules 1,2,3 ; la boule 4 est elle placée sur l'axe orthogonal à ce plan. Cela ne suffit pas, il faut déterminer les distances
 des boules 1,2, 3 à l'axe et la distance
des boules 1,2, 3 à l'axe et la distance  de 4 à l'origine. On délègue le calcul à l'outil de calcul symbolique.
de 4 à l'origine. On délègue le calcul à l'outil de calcul symbolique.
Ensuite on introduit toutes les forces de réaction : on les note 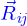 où
où 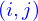 sont les indices de la numérotation décrite. On convient que l'ordre
sont les indices de la numérotation décrite. On convient que l'ordre 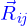 est la force que
est la force que  exerce sur
exerce sur 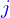 .
.
Il reste à écrire les équations d'équilibre de chaque boule, soit pour les forces
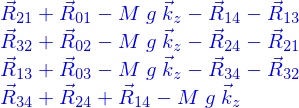
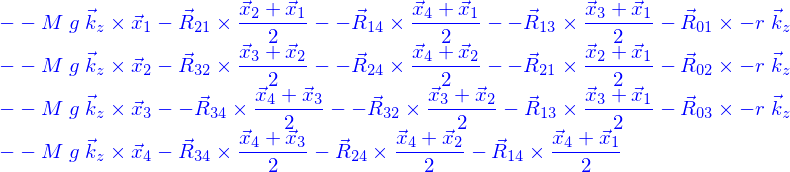
Ces expressions sont obtenues par un calcul dont le script est
addv(R)$
indices:flatten(map(lambda([%u],map(lambda([%v],concat(%u,%v)),[0,1,2,3,4])),[0,1,2,3,4]))$
Indicie(indices,R)$
assume(r>0,L>0)$
Boules:[[1,[(x1+x4)/2,-R14],[-r*kz,R01],[(x1+x2)/2, R21],[(x1+x3)/2,-R13],[x1,-M*g*kz]],
[2,[(x2+x4)/2,-R24],[-r*kz,R02],[(x2+x3)/2, R32],[(x2+x1)/2,-R21],[x2,-M*g*kz]],
[3,[(x3+x4)/2,-R34],[-r*kz,R03],[(x3+x1)/2, R13],[(x3+x2)/2,-R32],[x3,-M*g*kz]],
[4,[(x1+x4)/2, R14],[(x2+x4)/2, R24],[(x3+x4)/2, R34],[x4,-M*g*kz]]]$
EQF:map(lambda([%bi],apply("+",map(second,rest(%bi)))),Boules)$
EQC:map(lambda([%bi],apply("+",map(lambda([%xf],pv(%xf[1],%xf[2])),rest(%bi)))),Boules)$
On fabrique une structure de données pour les boules qui contient les forces et leur point d'application (pour simplifier, sans algorithmique pour la construire). Elle facilite l'écriture automatique des équations d'équilibre.
Il y a 8 équations vectorielles dont les inconnues sont les 9 vecteurs 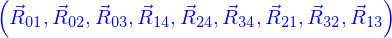 , soit donc 24 équations pour 27 variables scalaires.
, soit donc 24 équations pour 27 variables scalaires.
Mais on se doute qu'en situation de symétrie les 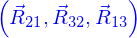 doivent être nulles (les boules 1, 2, 3 n'exercent pas de forces les unes sur les autres) alors que les
doivent être nulles (les boules 1, 2, 3 n'exercent pas de forces les unes sur les autres) alors que les 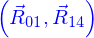 sont situées dans un plan vertical passant par
sont situées dans un plan vertical passant par  (de même pour les deux autres couples de forces).
(de même pour les deux autres couples de forces).
Ce qui fait qu'on peut paramétrer les forces comme
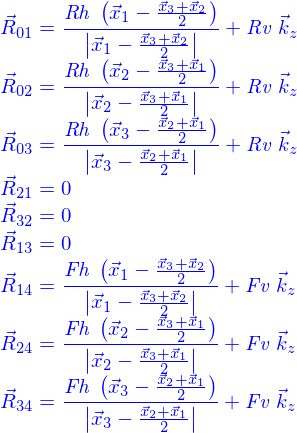
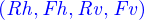 doivent être tels que les équations d'équilibre soient satisfaites. Le script est
doivent être tels que les équations d'équilibre soient satisfaites. Le script est
rnrm(%v):=%v/nrm(%v)$Indice([r,v],[F,R])$
CR:[R01=Rv*kz+Rh*rnrm((x1-(x2+x3)/2)),
R02=Rv*kz+Rh*rnrm((x2-(x1+x3)/2)),
R03=Rv*kz+Rh*rnrm((x3-(x1+x2)/2)),
R21=0,R32=0,R13=0,
R14=Fv*kz+Fh*rnrm((x1-(x2+x3)/2)),
R24=Fv*kz+Fh*rnrm((x2-(x1+x3)/2)),
R34=Fv*kz+Fh*rnrm((x3-(x1+x2)/2))
]@
On cherche donc à satisfaire ces équations d'équilibre. On obtient
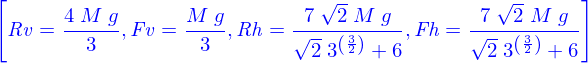
EQFC:flatten(map(lambda([%u],map(lambda([%k],xtav(ps(%u,%k))),[kx,ky,kz])),xtav(eval(EQF,CR,Pos))))@ EQRC:flatten(map(lambda([%u],map(lambda([%k],xtav(ps(%u,%k))),[kx,ky,kz])),xtav(eval(EQC,CR,Pos))))@ sol:ElVars(append(EQFC,EQRC),[Rv,Fv,Rh,Fh])@
Pourquoi ? Parce qu'on s'est contenté d'écrire des scripts individuellement contrôlables dans lesquels n'apparaissent aucuns calculs et qui ne font que spécifier des conditions. Le calcul effectif est entièrement délégué au soveur de l'outil utilisé.
L'outil est un logiciel de calcul symbolique. Par rapport à ce que restitue un script Matlab/Octave, elles ont l'avantage de pouvoir être lues sans que le cerveau derrière les yeux n'ait à analyser les valeurs numériques des variables. C'est aussi assez reposant !
Pour que ce soit en plus confortable, il est nécessaire que le travail se fasse dans un environnement qui le soit pour l'écriture pratique du script autant que pour sa soumission au logiciel qui l'interprète.
À moins que ça ait bien changé ces dernières années, le notebook de Mathematica (et sans doute de Maple) ne réalisent pas parfaitement cette condition. Il y a un notebook Maxima aussi qui s'appelle Wxmaxima qui souffre des mêmes inconvénients.
De mon point de vue il est bien préférable de disposer d'un outil qui permet à la fois d'écrire le script et de le transférer à son interpréteur. Et cet outil existe depuis longtemps, c'est Emacs.
On va maintenant expliquer comment faire des calculs comme celui qui vient de servir d'illustration en utilisant Emacs qui a été préalablement configuré pour communiquer à Maxima.
On montrera ensuite comment faire des calculs avec FreeFem++ au moyen d'une couche logicielle écrite en Maxima qui permet de manipuler les fonctionnelles au niveau symbolique de les transformer en un script FreeFem++ et d'exécuter les calculs (avec possibilité de récupérer les résultats sous Maxima).
Puis on expliquera comment incorporer des formules diverses sous format Maxima en Latex ainsi qu'en html. Emacs en communication avec Maxima permettant cela.
J'ai appelé ces éléments raccordés les uns aux autres :
Sinon, la mode actuelle est à Python, qui comporte des bibliothèques de calcul numerique Numpy, Scipy et même aussi une bibliothèque de calcul symbolique Sympy.
Les plus jeunes d'entre nous considéront donc que le fait d'utiliser des antiquités comme Emacs et Maxima (FreeFem++ aussi d'ailleurs, qui est une émanation de Modulef) est hautement suspect.
Ils ont bien raison !
Richard Stallman est un personnage attachant, doté d'une légende, qui a souvent été invité à donner son avis sur le sujet du logiciel libre et même sur d'autres sujets sans grands rapports.
Mais on reconnait la grandeur d'une œuvre à ce qu'elle dépasse les idées particulières de son auteur. De mon point de vue c'est le cas d'Emacs.
Emacs est un interpréteur Lisp doté de fonctionnalités poussées dans les entrées/sorties.
Une instance moderne d'Emacs se présente comme un Frame (c'est comme cela qu'on appelle une fenêtre du bureau dans Emacs) doté de menus qui permettent d'accéder (entre autre) à des fonctionnalités d'écriture de texte.
Il existe également ce qu'on appelle des modes. Par exemple il y a un mode Latex qui s'active dès lors que le nom de fichier du texte qu'on écrit a une extension « .tex ». Ce mode permet d'appeler Latex pour effectuer une compilation et il est même possible de visualiser le résultat obtenu sous forme pdf.
Comment cela fonctionne-t'il ?
On peut accèder au Lisp d'Emacs (appelé elisp) dans n'importe quelle fenêtre (les fenêtres dans Emacs sont des subdivisions de Frame) et donc on peut examiner comment lancer un process depuis Emacs.
Par exemple on écrit
(call-process "whoami" nil (current-buffer))puis on place le curseur à la ligne et on tape
C-x C-e(c'est à dire Control-appuyé 'x' puis toujours avec Control-appuyé 'e'). Et alors on voit apparaître qui la machine sur laquelle on travaille croit qu'on est (who do you think we are ?)
vinsardet sous Windows 10
chuwi-gerard\vinsard
Voilà ! On a lancé un process synchrone avec appel de la commande « whoami » et consigne de placer le résultat de cette commande dans l'espace dans lequel est écrit l'instruction « call-process » qu'on appelle un buffer.
À ce propos, Emacs sépare la fenêtre physique qu'on a sous les yeux de son contenu qui aurait pu apparaître dans une autre fenêtre. Ce contenu est souvent associé à un fichier mais ce n'est pas nécessaire. Le contenu de '*scratch*' n'est pas associé à un fichier.
On voit bien qu'il faut donner un nom générique à ce genre contenu qui n'est pas nécessairement celui d'un fichier. Et ce nom générique est buffer.
Cet appel de process peut être associé à une combinaison de touches. Pour cela on écrit
(defun whoami () (interactive) (call-process "whoami" nil (current-buffer))) (define-key global-map (kbd "C-a") 'whoami)On fait C-x C-e juste après la parenthèse fermante de defun et après celle de define-key (il y a une mécanisme de saut de curseur qui permet de voir quelles elles sont). Et pour la suite de la session, chaque fois qu'on tapera 'C-a' le répertoire courant du buffer où on est s'écrira à la position du curseur.
Voici en germe comment, par exemple, pourait fonctionner l'appel à la compilation Latex du mode Latex d'Emacs. En fait, ce n'est pas tout à fait cela, c'est plutôt un process asynchrone. Même si le lancement de Latex n'est pas emblématique de cela.
Un process asynchrone est un process indépendant de celui qui les lance (ici Emacs) mais avec lesquel ce dernier peut communiquer.
Si on tape 'esc x' (pour 'escape' puis 'x') on voit apparaître dans le petit espace du bas du frame 'shell'. Si on fait 'ret', on voit apparaître dans une des fenêtres du frame un shell (sous Unix) ou un cmd (sous Windows). On a lancé un process asynchrone.
Il y a plus de détails à donner pour décrire les instructions elisp lançant les process asynchrone, aussi ne le fera-t'on pas ici.
Par contre il est important de savoir qu'on peut le faire. Et qu'Emacs possède des instructions permettant de d'envoyer un ordre à ces process, comme (le process '*shell*' étant lancé)
(send-string "*shell*" "whoami\n")(on voit que la réponse de 'whoami' s'affiche dans le buffer '*shell*').
Emacs possède également un système de surveillance des sorties du process qu'il peut récupérer. C'est surtout cela qu'il serait un peu long de décrire. On se contente donc de l'idée que c'est possible.
Il reste bien des choses à dire sur Emacs. Mais ce minimum est suffisant pour comprendre le fonctionnement d'Appariteur.
D'une manière générale, le calcul symbolique n'est qu'un ensemble d'algorithmes qui admettent des expressions mathématiques en entrée et transforment celles-ci en autres expressions mathématiques.
Pour réaliser cela, il est nécessaire que les expressions mathématique soient codées
Ce codage est de la forme
On peut ainsi écrire des expressions composées. Par exemple
Cette forme est très facile à explorer pour un langage récursif (le lisp est apodictiquement récursif). Si on envoie
Un outil de calcul symbolique ne fonctionne pas autrement. D'une certaine façon il ne fait essentiellement que cela et tout ce qui vient en plus n'est qu'optionnel (accidentel).
Évidemment, sans ces options l'outil ne servirait presque à rien. Et ce sont elles qui déterminent son utilité.
Syntaxiquement, Maxima est tout à fait ordinaire. On trouve de nombreux tutorials, dont celui-ci qui fonctionne avec Wxmaxima (un maxima sous notebook à la Mathematica) et qui est une version ancienne du tutorial inclus dans Apapriteur.
Appariteur est une... disons customization d'Emacs qui
La connexion avec Maxima se fait en lançant un process asynchrone, la communication entre ce process et Emacs étant gérée par des fonctions de filtrage écrites en elisp.
Basiquement, on écrit un script Maxima dans 'wgb' et on dispose d'une série de combinaisons de touches qui envoient soit des morceaux entiers de textes (enclos par des balises '%%%;') soit une seule ligne soit une seule fonction à Maxima. Le résultat est affiché dans 'wbd' (sous le buffer 'jmaxima') comme si on l'y avait écrit directement (on peut d'ailleurs le faire).
les séparateurs d'instruction en Maxima sont '$' (exécuter l'instruction mais ne pas afficher le résultat) et ';' (exécuter et afficher). Appariteur ajoute '@' qui a pour effet que
Tout cela s'inspire de IMaxima qui est un mode d'Emacs. À une différence près : dans IMaxima c'est Maxima qui appelle Latex, dans Appariteur c'est Emacs. Cette modification permet plus de souplesse. Comme par exemple d'afficher du script ou l'image Latex du script selon les besoins.
L'insertion d'expressions mathématiques dans un fichier Latex se fait en écrivant entre balises l'expression sous le format Maxima. Une combinaison de touche permet d'envoyer l'expression à Maxima (cela s'affiche dans 'jmaxima'), de récupérer la chaîne de caractère en Latex et de l'insérer dans le fichier (là où elle doit l'être).
Il y a également un mécanisme analogue pour l'écriture en html (qu'on peut examiner sur cette page en regardant son fichier source (faire Control-U)). Ces mécanismes sont implémentés comme des 'hook' des modes Latex et html d'Emacs.
Pour FreeFem++, une bibliothèque Maxima d'Appariteur contient des fonctions driver des instructions de Freefem++. On utilise ces drivers pour écrire un script Maxima. FreeFem++ est appelé par une fonction Maxima ('FFgo()') qui écrit les instructions FreeFem++ dans un fichier et renvoie à Emacs le signal que FreeFem++ peut être appelé avec ce fichier en entrée. C'est alors ce que fait Emacs.
Voilà, l'essentiel est dit ! Appariteur n'est rien d'autre qu'une suite d'appels de process agencée de manière que le fonctionnement soit le plus commode possible.
Si ça peut aider, voici un dessin qui représente les relations entre Emacs, Latex et FreeFem++ qu'implante Appariteur
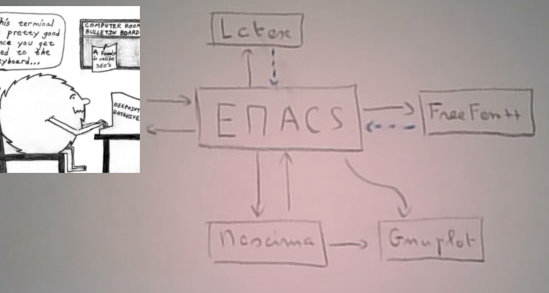
Et pour être tout à fait transparent, ces appels sont regroupés dans des fichiers contenant les fonctions Elisp ad hoc
Appariteur.el => l'organisation apparente d'Appariteur JMaxima.el => la connexion avec Maxima AppariteurHtml.el => Les hooks complétant le mode html d'Emacs AppariteurLatex.el => idem pour Latex Personnel.el => Les fonctions Elisp personnelles à l'utilisateur et son paramétrage d'Appariteur.et elles ont ajoutées à Emacs avec un appel
#!/bin/sh
cd chemin-du-repertoire-de-travail
emacs -Q -L chemin-du-repertoire-des-fichiers-.el --load Appariteur.el
Cette customization est proche de celle de Texmacs. Celle-ci qui n'a pourtant pas été utilisée. Du fait de sa lourdeur, il était plus simple de réécrire celles de ses fonctionnalités qui ont semblé utiles.
Maxima est doté de moins d'options que Mathematica et Maple mais son algorithmique interne (options incluses) n'est pas nécessairement moins efficace. Et il a l'avantage d'être ouvert. Ce qui permet de lui ajouter des options tant au niveau de la syntaxe externe des expressions qu'à celui de leur représentation lisp interne.
Et c'est ce que réalise CDE qui adjoint des facilités pour
CDE comporte également un composant qu'il partage avec Appariteur (qui pourrait tout à fait fonctionner sans Maxima) . La bibliothèque des fonctions qui transforment une expression en chaîne de caractère Latex. Ça peut paraître futile mais il est quand même bien plus agréable d'avoir sous les yeux l'expression telle qu'on l'écrirait à la main. La différence entre
cond([[x<-1,0],[[-1,0],1+x],[dans(x,IntOuv(0,1)),1-x]],0)et
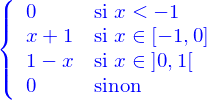
En dehors de ce composant (et encore), toutes les fonctions de CDE pourraient être codées dans un langage autre que celui de Maxima. Répétons-le, elle ne sont qu'un enrichissement fonctionnel.
Et le plus simple pour les décrire est encore de les mettre en situation.
La formule de Stokes donne la force de traînée 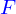 d'une bille sphérique de rayon
d'une bille sphérique de rayon  qui se déplace avec un mouvement rectiligne uniforme de vitesse
qui se déplace avec un mouvement rectiligne uniforme de vitesse  dans un fluide incompressible, d'étendue infinie et de viscosité
dans un fluide incompressible, d'étendue infinie et de viscosité  comme
comme

La question est de retrouver cette formule par le calcul. Pour cela il faut déjà calculer l'écoulement autour de la boule. C'est à dire résoudre le problème (de Stokes)

Puis exploiter ce champ de vitesse pour retrouver la formule.
On regarde le Batchelor On reprend le calcul On utilise des éléments finis
Dans le « An Introduction To Fluid Dynamics » de G.K. Batchelor. On trouve à la page 79
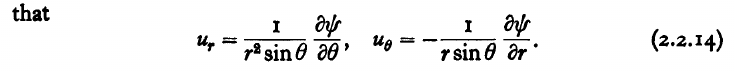
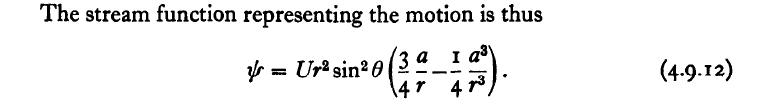
Sur ces pages, il est indiqué que les « spherical polar co-ordinates 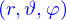 » sont utilisées. Donc du sphérique. Les vecteurs de base sont
» sont utilisées. Donc du sphérique. Les vecteurs de base sont
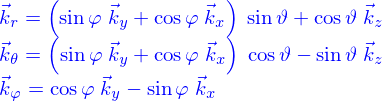
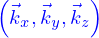 est une base orthonormée telle que la direction du déplacement de la bille est
est une base orthonormée telle que la direction du déplacement de la bille est 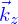 , la position par rapport au centre de cette bille est alors
, la position par rapport au centre de cette bille est alors 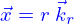 .
.
 est appelée la « stream function » ; on se dit qu'elle doit être telle que
est appelée la « stream function » ; on se dit qu'elle doit être telle que
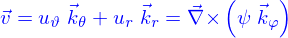
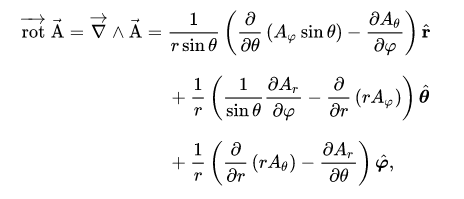
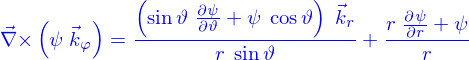
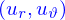 trouvées ne correspondent pas à celles de la formule 2.2.14 de Batchelor !
trouvées ne correspondent pas à celles de la formule 2.2.14 de Batchelor !
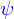 n'est pas la fonction telle que
n'est pas la fonction telle que 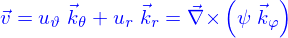 . Celle-ci est en fait
. Celle-ci est en fait 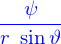 .
Effectivement on trouve que
.
Effectivement on trouve que
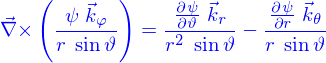
Les calculs du décrryptage de la fonction de courant donnée par Batchelor sont facilités par l'utilisation d'un système qui les fait automatiquement.
En plus de cela, on peut avoir envie de tracer la fonction de courant de Batchelor :
La voici et
voici celle où on se place dans le référentiel du fluide immobile
Le script de ce deux tracés est
PsiB:(a*(3*r^2-a^2)*sin(theta)^2)/(4*r)$ PsiBCyl:eval(PsiB,r=sqrt(r^2+z^2),sin(theta)=r/sqrt(r^2+z^2),a=1)$ FFldlc(tst,20,PsiBCyl,[z,-2,2],[r,-2,2], Cex=[[0,0,1]])$ FFldlc(tst,20,PsiBCyl-r^2/2,[z,-2,2],[r,-2,2], Cex=[[0,0,1]])$Il utilise le mailleur et le post-traitement de FreeFem++ pour tracer des lignes de niveau, ce qui a un meilleur rendu que celui d'une grille cartésienne et permet d'éliminer des zones, comme celle de l'intérieur de la bille.
Maintenant, il s'agit de retrouver la formule de Stokes à partir de cette fonction de courant (et de vérifier qu'elle correspond à un champ de vitesses qui satisfait bien au problème de Stokes). Mais les coordonnées sphériques sont pour cela plutôt une gêne qu'autre chose. Le mieux est de procéder de façon plus intrinsèque.
L'inspection de la fonction de courant donnée par Batchelor amène à la conclusion qu'elle s'écrit, à partir de la position 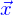 et de la direction de déplacement
et de la direction de déplacement 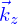 comme
comme

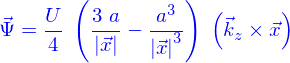
On obtient le champ de vitesses comme
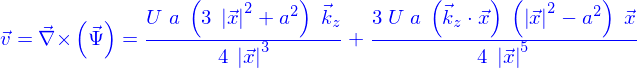
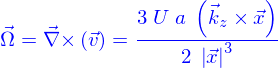
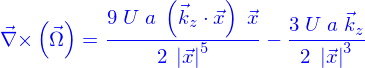
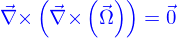
L'équation de Stokes 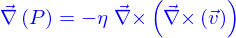 est donc valide. Il faut trouver
est donc valide. Il faut trouver  tel que
tel que
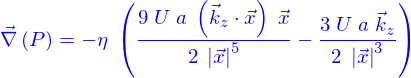
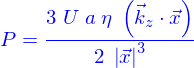
d'autre part, les conditions aux limites à l'infini sur le champ de vitesses sont bien satisfaites. Et en  on a
on a
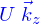
On vient de vérifier que la fonction de courant de Batchelor correspond bien au problème de Stokes.
Et cette vérification se fait avec ce script
Regles:[[grad(a),0],[grad(U),0],[grad(nrm(vx)^2),2*vx], [rot(pv(kz,vx)),2*kz],[rot(kz),0],[rot(vx),0], [grad(ps(kz,vx)),kz],[nrm(kz)^2,1]]$ symbolise(Psi,Omega)$addv(Psi,Omega)$ Psi:U/4*(3*a/nrm(vx)-a^3/nrm(vx)^3)*pv(kz,vx)$ vv:rtav(xtav(rot(Psi)))$ Omega:rtav(xtav(rot(vv)))$ rOm:rtav(xtav(rot(Omega)))$ rtav(xtav(rot(rOm)))$ P:3/2*U*a*eta*ps(kz,vx)/nrm(vx)^3$ rtav(xtav(grad(P)))$ assume(a>0)$En bref, CDE permet de faire des calculs différentiels sans coordonnées mais il faut lui fournir les règles appropriées au problème qu'on traite.
Pour trouver maintenant la formule de Stokes, on peut procéder de deux façons. Déjà par le calcul de la puissance dissipée dans tout l'écoulement comme
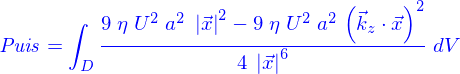
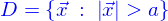 en posant
en posant 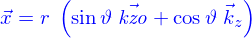 où
où 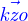 est un vecteur normal à
est un vecteur normal à 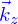 et de norme 1, on obtient
et de norme 1, on obtient

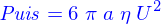
Un seconde méthode consiste à calculer le tenseur des contraintes
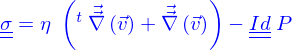
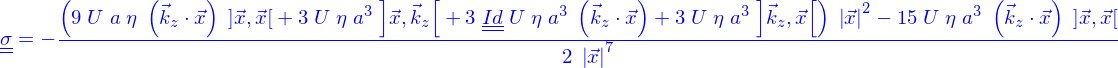
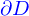 du domaine fluide, ce vecteur normal étant
du domaine fluide, ce vecteur normal étant
 on obtient
on obtient
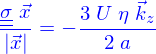
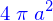 pour retrouver la formule de Stokes.
pour retrouver la formule de Stokes.
Le script qui fournit ces résultats est
Puis:xtav(Int3D(eta*nrm(rot(vv))^2,D))$
addv(kzo)$
Regles:[[grad(a),0],[grad(U),0],[grad(nrm(vx)^2),2*vx],
[rot(pv(kz,vx)),2*kz],[rot(kz),0],[rot(vx),0],
[grad(ps(kz,vx)),kz],[nrm(kz)^2,1],
[ps(kzo,kz),0],[nrm(kzo)^2,1],[Grad(vx),Id],[Grad(kz),0]]$
Puis1:trigsimp(xtav(ev(Puis,vx=r*(cos(theta)*kz+sin(theta)*kzo))))$
addy(sigma)$
sigma:xtav(-P*Id+2*eta*(Grad(vv)+Trans(Grad(vv)))/2)$
f:eval(rtav(ev(xtav(sigma*vx/nrm(vx)),nrm(vx)^2=a^2)),eval,nrm(vx)^2=a^2)
On n'a pas expliqué comment retrouver la fonction de courant à partir du problème de Stokes. On pourrait d'ailleurs le faire, mais ce n'est guère intéressant (on fait de la séparation de variables en sphérique).
Ce qui est par contre intéressant c'est de retrouver la formule de Stokes avec des moyens de calculs approximant le problème de Stokes par la méthode des éléments finis. Intéressant, parce que cela permet d'obtenir le moyen de calculer une telle formule pour autre chose qu'un bille isolée dans un fluide d'étendue indéfinie ou encore pour une bille mais dans un domaine fluide borné dans une direction. Par exemple dans un tube (le fluide n'est pas newtonien dans le film, mais qualitativement la bille descend de la même façon).
Pour éviter les considérations pré-adolescentes en matière d'éléments finis, le plus simple est de partir du modèle selon lequel le mouvement se fait de telle manière que la puissance dissipée dans le fluide par ce mouvement soit minimale.
Cette puissance dissipée s'écrit
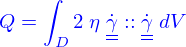
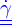 est le tenseur des vitesses de déformation. Pour
est le tenseur des vitesses de déformation. Pour 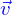 un champ de vitesse
un champ de vitesse
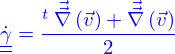
Le domaine fluide
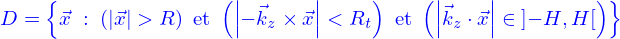
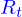 et de longueur
et de longueur  . Son bord est alors
. Son bord est alors
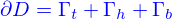
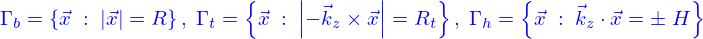
Les conditions aux limites sur  sont
sont
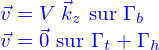
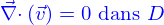
Le champ de vitesses est donc l'argument minimisant du problème
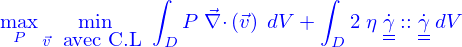
 , la pression, est le multiplicateur de Lagrange de la contrainte d'incompressibilité.
, la pression, est le multiplicateur de Lagrange de la contrainte d'incompressibilité.
Si on se limite au cas axisymétrique où le champ de vitesses est de la forme

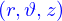 avec
avec 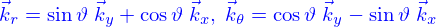 et avec des dépendances de
et avec des dépendances de 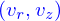 uniquement en
uniquement en 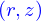 , les intégrales se réécrivent
, les intégrales se réécrivent
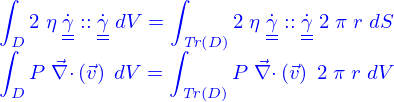
 ne dépend que de
ne dépend que de 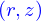
Un problème de ce genre est emblématique du champ d'application de la méthode des éléments finis. Il suffit de créer un maillage; d'approximer 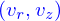 avec des polynômes de Lagrange de degrés 2 sur les triangles ;
avec des polynômes de Lagrange de degrés 2 sur les triangles ;  avec des polynomes de degrés 1 ; ces champs scalaires étant continus aux interfaces.
avec des polynomes de degrés 1 ; ces champs scalaires étant continus aux interfaces.
Et alors le problème se transforme en un système matriciel qu'il suffit de résoudre (avec une méthode moderne) pour trouver les valeurs des polynômes d'approximation et donc une représentation discrète de 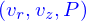 à partir de laquelle ont peut calculer des fonctionnelles. Comme par exemple la puissance dissipée où directement la valeur de force comme intégrale de la densité de forces issue du tenseur des contraintes.
à partir de laquelle ont peut calculer des fonctionnelles. Comme par exemple la puissance dissipée où directement la valeur de force comme intégrale de la densité de forces issue du tenseur des contraintes.
C'est le travail de FreeFem++ de s'occuper de ses taches. Et CDE a pour fonction d'améliorer encore la transparence entre la description qui précède et les résultats numériques qu'elle permet d'obtenir.
Voici un script Maxima qui fait ces calculs. C'est moche ! Mais le script en language de FreeFem++ (généré automatiquement) l'est encore plus...
(pour le maillage, on fait un petit dessin comme cela et on transcrit dans le format de la fonction FaitMaillage qui réalise toutes les étapes de cŕeation de maillage de FreeFem++)
Ses sorties sont
nbno = 9750 ; nbelv = 19141 ; nbindv= 1 , soit : 0 ; nbindl= 5 , soit : 1 2 3 4 5 Min Max de vr = -0.000242668 0.167379 Min Max de vz = -0.0364939 1 Min Max de P = -5.16474e-35 1884.62 (FV+FP)/FSto=-1.1427 ; Q/(FSto*V)=1.16092 ; FP/FSto=-0.765652 ; FV/FSto=-0.377047 ; Min Max de psi = -3.85494e-05 0.127127où on fait le rapport de la puissance dissipée calculée (Q) à la puissance issue de la formule de Stokes ; et le rapport de la force calculée avec le tenseur des contraintes (FV+FP : FV est la contribution visqueuse et FP celle de la pression) à la force de la formule de Stokes.
On ne retrouve pas le résultat de la formule de Stokes. C'est normal parce que si grand soit le domaine de calcul utilisé, il n'est pas infini. Et le champ des vitesses du calcul en domaine infini correspond à un débit infini qui ne peut se réaliser qu'avec un domaine de calcul infini (ou des conditions aux limites qui simulent l'infini derrière elles, ce qu'on n'a pas cherché à implanter).
Mais c'est sans importance pour le propos qui se borne à présenter un outil de calcul. Lequel permet d'obtenir les sortie de FreeFem++ ainsi que diverses visualisations comme vr, vz, P, fonction de courant.
Il resterait à décrire comment peuvent être récupérées les sorties de FreeFem++ sous forme de valeurs données à des variables de Maxima. Mais cela demanderait la description du protocole d'une façon plus complexe de lancer FreeFem++ qui est un peu longue à faire.
La chaîne élastique est représentée comme une association de masse et ressorts comme ici.
On suppose que la longueur à vide des ressorts est  ; leur raideur
; leur raideur 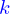 ; la valeur des masses
; la valeur des masses  .
.
Il y a  masses numérotés de 1 à
masses numérotés de 1 à  et donc
et donc 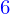 ressorts. Et aucune contrainte d'extrémité.
ressorts. Et aucune contrainte d'extrémité.
Dans ce cas l'énergie cinétique est
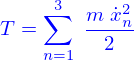
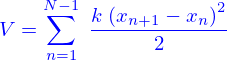
 ; ses degrés de liberté sont les
; ses degrés de liberté sont les 
 auxquels sont associées les vitesses
auxquels sont associées les vitesses 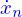 .
.
On peut obtenir les équations du mouvement de ces masses avec les  équations d'Euler-Lagrange sur les couples
équations d'Euler-Lagrange sur les couples 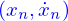
Elles sont linéaires et donc on peut envisager de les intégrer analytiquement après les avoir adimensionnées. Si on fait 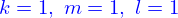 les
les  sont ramenés à
sont ramenés à  et le temps
et le temps  à
à  .
.
Par exemple, pour 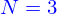 on obtient
on obtient
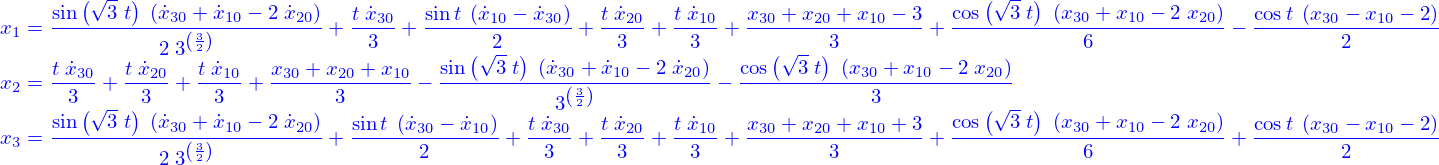
 et
et 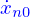
Et les expressions deviennent évidemment encore plus volumineuse au fur et à mesure qu'on augmente  . Et pire encore, on arrive rapidement à une situation où celui du solveur de Maxima qui utilise la méthode de Laplace ne sait plus trop bien retrouver les originaux. L'autre, qui utilise les exponentielles de matrices n'est guère plus brillant.
. Et pire encore, on arrive rapidement à une situation où celui du solveur de Maxima qui utilise la méthode de Laplace ne sait plus trop bien retrouver les originaux. L'autre, qui utilise les exponentielles de matrices n'est guère plus brillant.
Il est finalement plus simple (et pas beaucoup plus imprécis) d'utiliser une méthode numérique de type Dormand Prince (d'ordre 4/5) pour l'intégration des équations.
Ce qu'on veut obtenir avec ce problème c'est une confirmation d'expérimentation numérique du théorème du viriel qui affirme que la valeur moyenne des énergies potentielles et cinétiques finissent par coïncider.
Et l'intérêt de l'approche est qu'elle donne une idée du temps nécessaire pour que ce résultat soit approximativement valable.
On garde l'adimensionnement, on choisit 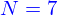 , on prend comme valeurs initiales toutes les vitesses nulles et les positions
, on prend comme valeurs initiales toutes les vitesses nulles et les positions 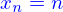 sauf
sauf qui est mise à
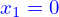 .
.
On obtient alors le tracé des 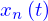 . Mais surtout celui des valeurs moyennes des énergies cinétique et potentielle à partir duquel on peut voir qu'en un temps de
. Mais surtout celui des valeurs moyennes des énergies cinétique et potentielle à partir duquel on peut voir qu'en un temps de 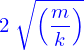 il y a quasiment la coïncidence cherchée.
il y a quasiment la coïncidence cherchée.
Le script qui permet de faire cela est le suivant
N:7$symbolise(X)$
X:map(first,Indicie(makelist(i,i,1,N),x))@Xp:apply(dotise,X)@
T:apply("+",map(lambda([%u],1/2*m*%u^2),Xp))@
V:apply("+",map(lambda([%u,%v],1/2*k*(%u-%v-l)^2),rest(X),rest(X,-1)))@
L:T-V@
data:[k=1,m=1,l=1]$
SM:ev(EquationLagrange(L,0,[],[],X,Xp),eval)@
SM:ev(append(SM,[(T-Tb)/t,(V-Vb)/t]),data)@
EDO:[append(X,Xp,[Tb,Vb]),SM,[]]$
Prepare(EDO)$ lX:[]$
X0:makelist(i,i,1,length(X))$ Xp0:makelist(0,length(Xp))$
X0[1]:0@
Vb0:ev(V,map("=",X,X0),data)@ Tb0:ev(T,map("=",Xp,Xp0),data)@
XXp0:append(X0,Xp0,[Tb0,Vb0])@
TestSTA(0.001,XXp0)@
tol:1.0e-6$
SEDO(XXp0,0.001,5,200)$
apply(XvsT,append([EDO],Xp))$
apply(XvsT,append([EDO],X))$
apply(XvsT,ev(append([EDO],[T,V]),data))$
apply(XvsT,ev(append([EDO],[Tb,Vb]),data))$
Sa longueur vient surtout de l'ajout aux EDOs des variables 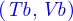 qui permettent le calcul des valeurs moyennes.
qui permettent le calcul des valeurs moyennes.
Voilà... Je ne sais pas si j'ai été bien clair mais le message essentiel est que le calcul devient presque agréable dès lors qu'on le délègue pour se concentrer sur les résultats qu'il amène.
Cette délégation peut être d'humain à humain (le maître dit à son esclave de faire le calcul).
Mais aussi d'humain à machine. Celles-ci (les machines) ont les inconvénients de leur avantage. Elles sont fiables (ou tout du moins il est possible de les rendre fiables) mais elles opèrent sur des données codées et l'effort à faire pour rendre ces données intelligibles n'est pas négligeable.
Il est donc intéressant d'adjoindre des systèmes de décodage automatique (de codage aussi d'ailleurs) aux algorithmes qu'on utilise.
Et cela dès qu'on commence à les mettre au point. C'est surtout dans les débuts d'un calcul que c'est utile.
C'est d'ailleurs ce que vendent les logiciels commerciaux. Les algorithmes sont publics mais pas leur interface.
On peut donc se passer d'eux si on maîtrise la technique du codage/décodage et de l'appel de process ad hoc.